Logique combinatoire et logique séquentielle
Logique combinatoire
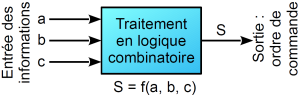
Une commande est dite combinatoire, lorsqu'à chacune des combinaisons d'entrées correspond un seul état de la sortie, et toujours le même !
Remarque : Les opérateurs logiques (OU, NAND, etc..) font partie de la logique combinatoire.
Logique séquentielle
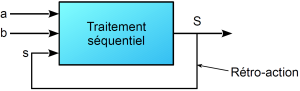
Dans une logique séquentielle, plusieurs combinaisons identiques de variable d'entrées peuvent donner des états de sortie différents.
L'état de sortie est donc nécessairement pris en compte.
Le mot séquentiel vient du latin « sequentia » qui signifie suite. Le traitement séquentiel est donc une suite d'états différents qui dépendent de 1'état qui précède.
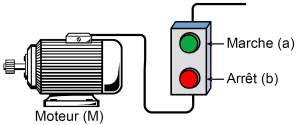
Exemple : Commande d'un moteur par boutons-poussoirs
Soit un moteur « M » commandé par un contacteur « KM » à l'aide de deux boutons-poussoirs marche « a » et arrêt « b ».
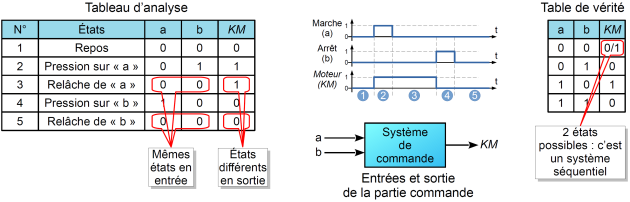
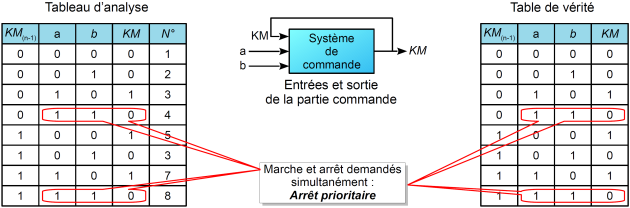
Le tableau d'analyse ci-dessous indique aux lignes 3 et 5 des états identiques en entrée (a = 0 et b = 0) alors que la sortie « KM » est à l'état 1 ligne 3 et à l'état 0 ligne 5 ...
Dans la table de vérité ci-dessous résume le tableau d'analyse en faisant apparaître pour les états d'entrée (a = 0 et b = 0) une sortie « KM » à l'état « 0 ou 1 ».
On a donc bien un système séquentiel !
Pour établir la table de vérité de ce fonctionnement séquentiel, on doit faire appel à une variable d'entrée supplémentaire.
Cette variable supplémentaire « KM(n-1) » permettra de prendre en compte l'état de la sortie « KM » juste avant le nouvel état des entrées (instant n-1). Ceci permet de différentier les fonctionnements des lignes 3 et 5 du tableau d'analyse.
On parle de variable interne, de variable secondaire ou de variable d'état.
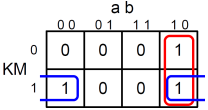
Équation déduite du tableau de Karnaugh : 
Après factorisation de l'équation : 
