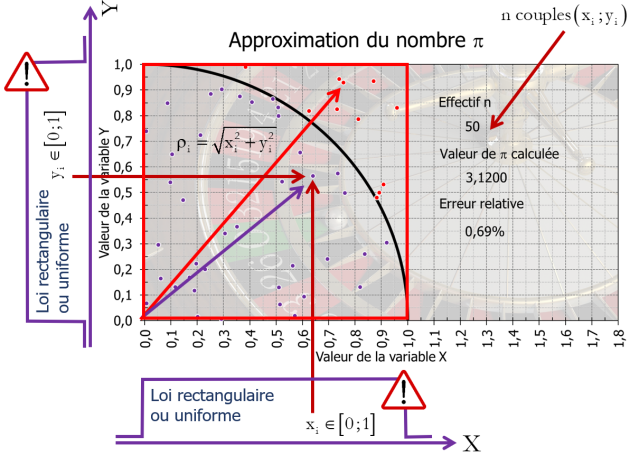
Exercice : Estimation du nombre \(\pi\)
Pour estimer le nombre \(\pi\), on a besoin encore une fois d'un modèle de mesure et d'une fonction de mesure. Ce modèle de mesure va faire apparaître deux grandeurs : d'une part la surface d'un carré d'arêtes unitaires et d'autre part à la surface d'un quart de disque s'appuyant sur ce carré.
La surface du quart de disque est égale à \(\dfrac{\pi}{4}\) si on a un rayon unitaire. Ce quart de disque s'appuie intégralement dans le carré.
Donc, pour estimer la valeur du nombre \(\pi\), on va dire que \(\dfrac{\pi}{4}=\dfrac{\textcolor{violet}{\text{Surface violette}}}{\textcolor{red}{\text{Surface rouge}}}\).
Donc \(\pi=4 \times \dfrac{\textcolor{violet}{\text{Surface violette}}}{\textcolor{red}{\text{Surface rouge}}}\).
Ceci est le modèle de mesure. C'est la description du mesurande \(\pi\).
Question
En utilisant la méthode random de la bibliothèque random, réaliser un programme qui permet d'estimer la valeur de \(\pi\) pour \(n\) valeurs aléatoires générées.
# Importation de la bibliothèquefrom random import random as rd
Indice
Créer une variable contenant le nombre de valeurs aléatoires.
Indice
Créer un compteur initialisé à 0.
Indice
Créer une boucle répétée pour le nombre de valeurs aléatoires désirées :
créer 2 variables x et y dans lesquels sont stockés des valeurs aléatoires (comprises entre [0 ;1]) obtenues avec la méthode random.
si le point de coordonnée (x ;y) appartient au cercle, incrémenter le compteur.
Indice
Faire l'estimation du nombre \(\pi\) à partir du produit de 4 par le rapport du compteur sur le nombre total de valeurs.