Stabilité d'une structure et isostatisme
Degrés de liberté – Isostatisme – Hyperstatisme
Un solide rigide isolé dans l'espace peut se déplacer librement dans un mouvement qu'on peut décomposer suivant 6 transformations géométriques indépendantes (translations et rotations autour d'axes fixes dans deux directions d'une base liée à notre espace à 3 dimensions). Il en est de même d'un solide isolé par rapport à un autre référent.
Si ces solides sont liés mécaniquement, certains de ces mouvements élémentaires sont impossibles. On appelle degrés de liberté dans une liaison, les mouvements relatifs indépendants d'un solide par rapport à l'autre autorisés par cette liaison.
Pour chaque type de liaison considérée, il résulte une combinaison différente des degrés de liberté, dépendant complètement de la géométrie des contacts de liaison.
On parle d'isostatisme lorsqu'une structure ou un mécanisme ne sont pas contraints excessivement, c'est-à-dire qu'aucun des degrés de liberté n'est supprimé par 2 liaisons différentes soient internes à l'assemblage, soit vis-à-vis de l'assemblage vers l'extérieur.
Une structure est dite hyperstatique si au moins un degré de liberté d'un élément d'une structure est supprimé par 2 liaisons différentes.
Le degré d'hyperstatisme d'une structure est le nombre de liaisons à supprimer pour obtenir une structure isostatique.
Approche de problème plan
Toutes les structures étudiées étant planes, L'iso / hyperstatisme est donc analysé d'après les 3 degrés de libertés restant (à savoir les 2 translations Tx et Ty dans le plan et la rotation Rz autour de l'axe z (perpendiculaire au plan). Il existe 3 types de liaisons :
appui simple qui supprime la translation Ty au niveau de la liaison
articulation qui supprime les 2 translations Tx et Ty au niveau de la liaison, mais pas la rotation Rz
encastrement qui supprime au niveau de la liaison les 3 degrés de liberté.
Le nombre d'inconnues de liaison est lié directement au nombre de degrés de liberté supprimés.

Stabilité des structures (stabilité géométrique)
On dit qu'un ouvrage est stable géométriquement s'il est isostatique, ou hyperstatique. En revanche, Il est instable s'il est hypostatique et cela conduit à la ruine du bâtiment.
Hypostatique si : 3 × nombre de barres – somme des inconnues de liaison > 0
Isostatique si : 3 × nombre de barres – somme des inconnues de liaison = 0
Hyperstatique si : 3 × nombre de barres – somme des inconnues de liaison < 0
Exemple : Système hypostatique
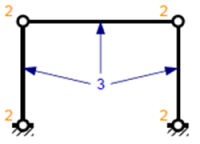
Soit une structure composée de 3 éléments, tous articulés.
Nombre de barres : 3
Nombre d'inconnues de liaison : 2 (car articulation) × 4 = 8
3 × 3 – 8 = 1 > 0 Le système est hypostatique.
C'est un parallélogramme déformable. Il faut donc rajouter un élément assurant la stabilité.
Exemple : Système isostatique
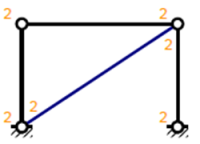
Soit une structure composée de 4 éléments, tous articulés.
Nombre de barres : 4
Nombre d'inconnues de liaison : 2 (car articulation) × 6 = 12
3 × 4 – 12 = 0
Le système est isostatique.
Exemple : Système hyperstatique
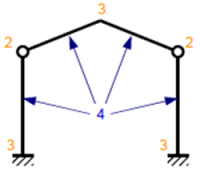
Soit un portique composé de deux poteaux et de deux traverses encastrées au faîtage. Les pieds de poteau sont encastrés.
Les liaisons tête de poteau / traverse sont des articulations.
Nombre de barres : 4
Nombre d'inconnues de liaison : 3 + 2 + 3 + 2 + 3 = 13
3 × 4 – 13 = –1 < 0
Le système est hyperstatique d'ordre 1.
Remarque : Hyperstaticité
L'hyperstaticité d'une structure peut induire des contraintes dans l'assemblage des éléments. Il faut bien maîtriser ce paramètre en construction.