La logique combinatoire

La table de vérité

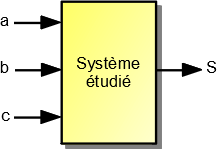
La table de vérité permet de connaître l'état des sorties pour chaque combinaison des variables d'entrée. Le fonctionnement est décrit par une équation logique qui utilise les opérateurs logiques.

Chaque variable ayant 2 états (0 ou 1) il y a 2N lignes où N est le nombre d'entrées, soit ici 23 = 8 lignes.

Exemple

Table de vérité

c

b

a

S

0

0

0

0

0

1

0

0

1

1

2

0

1

0

1

3

0

1

1

1

4

1

0

0

0

5

1

0

1

0

6

1

1

0

0

7

1

1

1

0

ÉQUATION EXTRAITE DE LA TABLE DE VÉRITÉ (DESCRIPTION LITTÉRALE)

Il faut lister toutes les lignes où « S = 1 »

  • Ligne 1 : (l'entrée « c » est à l'état 0) ET [(l'entrée « b » est à l'état 0) ET (l'entrée « a » est à l'état 1)]

  • Ligne 2 : (l'entrée « c » est à l'état 0) ET [(l'entrée « b » est à l'état 1) ET (l'entrée « a » est à l'état 0)]

  • Ligne 3 : (l'entrée « c » est à l'état 0) ET [(l'entrée « b » est à l'état 1) ET (l'entrée « a » est à l'état 1)]

 

RÈGLE D'ÉCRITURE :

  • Lorsque la variable d'entrée « a » est à l'état 1, elle se note : a color blue {bold a}

  • Lorsque la variable d'entrée « a » est à l'état 0, elle se note : a ¯ color blue {bold bar a} (on lit a barre)

  • Le « OU » se traduit par le symbole : + color blue {"+"} (on lit OU)

  • Le « ET » se traduit par le symbole : • color blue {bold "•"} (on lit ET)

 

ÉQUATION EXTRAITE DE LA TABLE DE VÉRITÉ

S = c ¯ . b ¯ . a + c ¯ . b . a ¯ + c ¯ . b . a color blue { S=bar c . bar b . a + bar c . b . bar a + bar c . b . a }

 

SIMPLIFICATION DE L'ÉQUATION

S = ( a + b ) . c ¯ color blue {S=(a+b). bar c }

C'est une équation associant des fonctions logiques de base ( NON, ET, OU,..).

On lit « S égale a OU b ET c barre ».