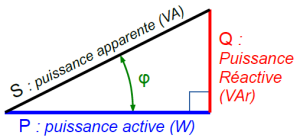
La puissance active est la puissance réellement disponible pour exécuter le travail sous forme de chaleur, mécanique, lumière. Elle se mesure en watts (W).

En triphasé sinusoïdal : \(\textcolor{blue}{\mathbf{ \large{P = U \times I \times \sqrt{3} \times cos  \varphi}}}\)    avec \(\left\lbrace \begin{array}{lll} \text{P : puissance active en Watt (W)} \\\text{U : tension d'alimentation en Volt (V)} \\\text{I : intensité du courant en Ampère (A)} \\ \varphi \text{ : déphasage entre le courant et la tension} \\ cos \varphi \text{ : facteur de puissance} \end{array} \right.\)

La puissance réactive représente la puissance engendrée par les éléments réactifs du circuit, qui sont des condensateurs (réactance capacitive) ou des bobines (réactance inductive). La puissance réactive ne consomme pas d'énergie, mais n'effectue aucun travail. Elle se mesure en voltampères réactifs (VAr)

triphasé sinusoïdal  : \(\textcolor{blue}{\mathbf{\large{ Q= U \times I \times \sqrt{3} \times sin \varphi}}}\)    avec \(\left\lbrace \begin{array}{lll} \text{Q : puissance réactive en Volt Ampère réactif (VAr)} \\\text{U : tension d'alimentation en Volt (V)} \\\text{I : intensité du courant en Ampère (A)} \\ \varphi \text{ : déphasage entre le courant et la tension} \end{array} \right.\)

Si l'on connaît la puissance active : \(\textcolor{blue}{\mathbf{ \large{Q = P \times tan \varphi}}}\)