Déphasage et facteur de puissance
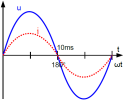
Tension et courant sinusoïdaux
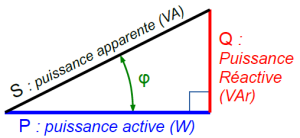
Le facteur de puissance « cosφ » image l'utilisation qui est faite de l'énergie fournie par le réseau.
\(\definecolor{mycolor}{rgb}{1, 1, 0.8} \fcolorbox{red}{mycolor}{$ \mathbf{\large{cos \varphi = \frac {P}{S}}}$}\)
Si cosφ=1 (récepteur résistif), pour une tension et un courant donnés, on obtient alors la puissance active maximale. Si ce n'est pas le cas, la puissance moyenne « P » est inférieure au produit « U x I ».
Dans le cas d'un récepteur, le facteur de puissance est compris entre 0 et 1.
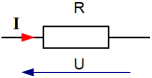
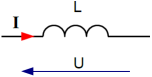
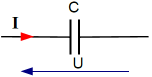
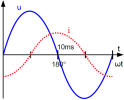
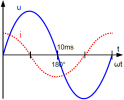
Récepteur purement résistif | Récepteur purement inductif | Récepteur purement capacitif |
|---|---|---|
|
|
|
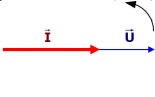
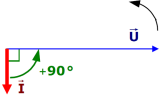
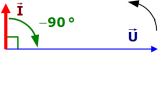
Déphasage : φ = 0° | Déphasage : φ = +90° | Déphasage : φ = -90° |
Puissance active : \(\mathbf{ P = U \times I \times cos \varphi = U \times I = S}\) car cosφ = cos(0°) = +1 | Puissance active : \(\mathbf{ P = 0 W}\) car cosφ = cos(+90°) = 0 | Puissance active : \(\mathbf{ P = 0 W}\) car cosφ = cos(-90°) = 0 |
Puissance réactive : \(\mathbf{ Q= 0 VAr}\) car sinφ = sin(0°) = 0 | Puissance réactive : \(\mathbf{ Q= U \times I \times sin \varphi = U \times I = S}\) car sinφ = sin(+90°) = +1 | Puissance réactive : \(\mathbf{ Q= U \times I \times sin \varphi = U \times I = S}\) car sinφ = sin(-90°) = -1 |
Représentation vectorielle (Fresnel)
| Représentation vectorielle (Fresnel)
| Représentation vectorielle (Fresnel)
|