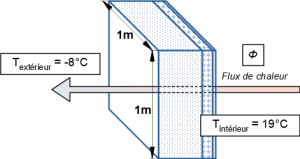
Le flux thermique
Le flux thermique « Φ » représente la quantité d'énergie (ou plutôt la « puissance ») passant par une paroi (en W). Pour généraliser la formule, on considère que « Φ » représente les flux passant par l'ensemble des parois d'un bâtiment. Il s'agit des déperditions conductives totales :
\(\mathbf{\large {\Phi = \sum (U \times S \times \Delta T )}}\)
Le flux thermique Φ (W) qui traverse un matériau dépend de l'écart de température entre ses deux faces.
\(\definecolor{mycolor}{rgb}{1, 1, 0.8} \fcolorbox{red}{mycolor}{$\mathbf{\large{\Phi = \frac {1}{R} \times S \times \Delta T = U \times S \times \Delta T = D \times (T_{int} - T_{ext})}}$}\)
Φ : flux thermique en Watt (W)
S : surface de la paroi (m²)
R : résistance thermique de la paroi (m².K·W-1)
U : coefficient de transmission thermique de la paroi (W·m-2·K-1)
D : Déperdition thermique de la paroi (W·K-1)
ΔT : différence de température entre l'intérieur et l'extérieur en Kelvin (K) ou en degré Celsius (°C)
Tint : température intérieure en Kelvin (K) ou en degré Celsius (°C)
Text : température extérieure en Kelvin (K) ou en degré Celsius (°C)
Si on connaît le flux à travers une paroi et la température intérieure, il est possible de déterminer la température en sortie de paroi :
\(\definecolor{mycolor}{rgb}{1, 1, 0.8} \fcolorbox{red}{mycolor}{$\mathbf{\Large{T_{ext} = T_{int} - \frac {R \times \Phi}{S}= T_{int} - \frac {\Phi}{D}}}$}\) avec \(\left\lbrace\begin{array}{lll} \phi\text{ : Flux thermique en Watt (W)} \\ \text{R : résistance thermique }(m^{2} \cdot K \cdot W^{-1}) \\ \text{S : surface de la paroi }(m^{2}) \\ \text{U : déperdition thermique }(W \cdot K^{-1}) \\ T_{ext} \text{ : température extérieure en Kelvin (K) ou en degré Celsius (°C)} \\ T_{int} \text{ : température intérieure en Kelvin (K) ou en degré Celsius (°C)}\end{array} \right.\)