Gradateurs
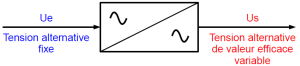
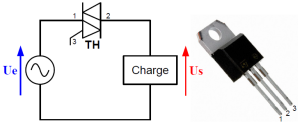
Le schéma de principe de ce convertisseur est présenté ci-contre. Il s'agit d'un interrupteur commandé qui laisse ou non passer le courant. L'objectif est de faire varier la valeur efficace de la tension aux bornes de la charge.
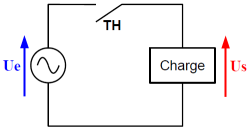
Deux techniques sont le plus souvent utilisées pour la commande du triac :
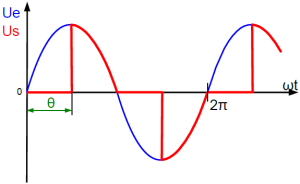
![]() Gradateur à angle de phase : la commande par « angle de phase » pour les charges à faible inertie (éclairage)
Gradateur à angle de phase : la commande par « angle de phase » pour les charges à faible inertie (éclairage)
Nous pouvons déterminer la puissance moyenne fournie à une charge purement résistive : \(\mathbf{\large{\bar{P} = P_{moy} = \frac {U^{2}}{R}} \times (1 \times - \frac {\theta}{\pi} + \frac {sin 2 \theta}{2 \pi})}\)
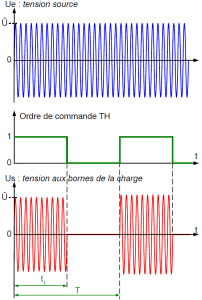
![]() Gradateur à train d'ondes : réservé aux charges à forte inertie (systèmes thermiques : chauffage d'un volume de solide, d'un débit de liquide ou de gaz) souvent associés à une régulation permettant de maintenir une température à une valeur de consigne.
Gradateur à train d'ondes : réservé aux charges à forte inertie (systèmes thermiques : chauffage d'un volume de solide, d'un débit de liquide ou de gaz) souvent associés à une régulation permettant de maintenir une température à une valeur de consigne.
Le circuit de puissance du gradateur à train d'ondes est identique à celui d'un gradateur à angle de phase. Seule l'électronique de commande est différente.
La durée du signal de commande appliqué sur les gâchettes des semi-conducteurs (Triac) permet de moduler l'énergie. Dans le cas d'une régulation de température, l'information issue du régulateur module le temps « t1 ». Le cycle se répète à chaque période « T ».
On obtint une alternance d'un train d'ondes sinusoïdales (de durée « t1 ») avec une absence de tension sur une période de quelques secondes.
La puissance délivrée dépend du rapport cyclique : \(\mathbf{\large{\alpha = \frac {t1}{T}}}\)
Nous pouvons déterminer la puissance moyenne fournie à une charge purement résistive : \(\mathbf{\large{\bar{P} = P_{moy} = \alpha \times (\frac {U^{2}}{R}})= \alpha \times P_{nominale}}\)
Performances : ce procédé de modulation d'énergie ne dégrade pas le facteur de puissance de l'installation