Essai de traction
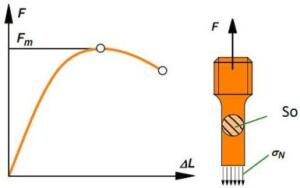
Un essai de traction est une expérimentation qui permet de mesurer le degré de résistance à la traction \(R_{m}\) d'un matériau.
L´essai de traction permet de caractériser les matériaux, indépendamment de la forme de l'objet sollicité. Cet essai consiste à placer une petite barre (éprouvette) du matériau à étudier entre les mâchoires d'une machine de traction qui tire sur cette barre jusqu'à sa rupture. L'essai de traction est donc un essai destructif. On enregistre l'allongement et la force appliquée, que l'on convertit ensuite en déformation et contrainte.
La force d'essai maximale \(F_{m}\) ainsi générée est une mesure pour la résistance du matériau.
La résistance à la traction \(R_{m}\) est calculée à partir de la force d'essai maximale \(F_{m}\) et de la section transversale initiale \(S_{0}\) de l'échantillon.
\(F_{m}\) : force maximale d'essai en N
\(S_{0}\) : section initiale en mm2
\(R_{m}\) : résistance à la traction en N/mm2
\(R_{m} = \frac{F_{m}}{S_{0}}\)
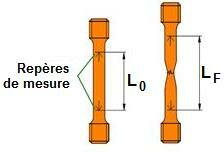
L'allongement à rupture A% caractérise la ductilité d'un matériau c'est-à-dire son aptitude à se déformer plastiquement sans se rompre : plus A% est grand, plus le matériau est ductile.
\(A\%\) : allongement à rupture en %
\(L_{0}\) : longueur initiale en mm
\(L_{F}\) : longueur après la rupture en mm
\(A\% = \frac{L_{F} - L_{0}} {L_{0}} 100\)
Remarque : Ductilité
La ductilité des matériaux est mise à profit avec le procédé d'emboutissage, technique de fabrication permettant d'obtenir, à partir d'une feuille de tôle plane et mince, un objet dont la forme n'est pas développable. L'emboutissage est notamment utilisé dans l'industrie automobile, en électroménager, ...
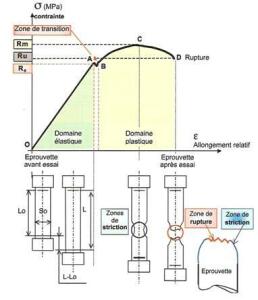
Lors d'un essai de traction, on enregistre la courbe \(\sigma = f(\epsilon)\) de l'intensité de l'action mécanique en fonction de l'allongement de l'éprouvette.
En abscisse, l'allongement relatif, \(\epsilon = \frac{\Delta L}{Lo}\) (utilisable dans le domaine élastique)
En ordonnée, la contrainte Sigma : \(\sigma\)
\(F\) est la force exercée en [N].
\(S_{0}\) est la section droite initiale (en mm²).
Ainsi, la résistance limite élastique Re :
\(R_{e} = \sigma_{e} = \frac{F_{e}}{S_{0}}\)
et toujours dans le domaine élastique :
\(\sigma_{e} = E \times\epsilon\)
Sans parler de la zone de transition, le tracé fait apparaître les domaines suivants :
Le domaine élastique : Pour tous les points du segment [OA], la déformation est proportionnelle à la contrainte.
La suppression de la charge entraîne la suppression de la déformation, l'éprouvette reprend sa forme et sa dimension d'origine.
Dans cette zone, la loi de Hooke traduit le comportement élastique du matériau : \(\sigma = E \times \epsilon\)
\(E\) est le module d'élasticité ou module de Young, exprimé en MPa (Méga Pascal) ou en N/mm².
Le domaine plastique : zone [BC]. L'allongement n'est plus proportionnel à l'effort appliqué : à la suppression de la charge, il reste une déformation, l'éprouvette ne reprend pas sa longueur initiale.
Le point C correspond à une intensité \(R_{m}\) qui est la contrainte maximale que l'éprouvette ne doit pas dépasser pour conserver ses propriétés.
La zone de striction : zone [CD]. On relâche l'effort appliqué mais l'allongement continue de croître. Il apparaît un étranglement appelé striction qui s'accentue jusqu'à la rupture en D.
Remarque : Elasticité
Les ressorts utilisent le comportement élastique du matériau qui les constitue. Ils se déforment quand ils sont soumis à un effort et reprennent leur forme et leurs dimensions initiales quand la sollicitation disparaît. Certains travaillent en compression, d'autres en traction.