Introduction au filtrage : Analyse fréquentielle d'un signal - Analyse de Fourier
Définition : Analyse de Fourier - Spectre
Joseph Fourier, un mathématicien, a mis en évidence en 1822 le fait que tout signal est la somme de signaux sinusoïdaux et cosinusoïdaux.
Pour représenter la composition spectrale d'un signal (spectre en fréquence), on utilise un système d'axes graduésen amplitude (axe des ordonnées) et en fréquence (axe des abscisses). Chaque fréquence est représentée par un trait vertical dont la hauteur est proportionnelle à l'amplitude du signal. Ce système d'axe est appelé un spectre.
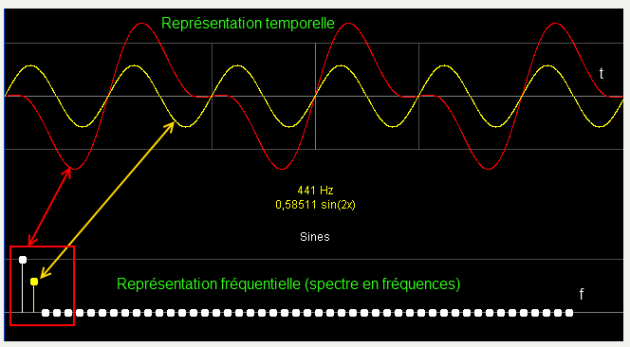
Exemple : Décomposition du signal
Dans l'exemple ci-dessus le signal rouge à pour équation :
v(t) = sin(x) + 0,58.sin(2x)
Avec x= 2.π.220.t car il est la somme de deux tensions sinusoïdales de fréquence 220Hz et 440Hz.
Fondamental : Fréquences fondamentales et harmoniques
Dans une décomposition de Fourier la fréquence la plus basse, hormis la composante continue est appelée Fréquence fondamentale et généralement notée f.
Les fréquences suivantes, multiples de f sont appelées des harmoniques.