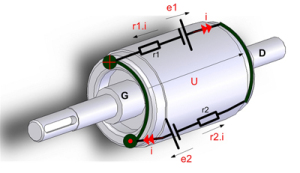
Justification de la construction en cage d'écureuil
Chaque conducteur placé sous un pôle est le siège d'une force électromotrice (f.e.m.). Dans le cas du schéma ci-contre les deux f.e.m s'ajoutent.
Hypothèses liées à la construction du moteur (symétries géométriques et électriques) :
e1 = e2 = e et r1 = r2 = r
Écrivons la loi des mailles pour démontrer que les liaisons en G et D sont bien au même potentiel :
e1 - r2 × i + e2 - r1 × i = 0
-2 r × i + 2 . e = 0
d'où i = e / r
Conducteur supérieur -r1 . i + e1 - U = 0 U = e - r . i U = e - r . (e / r) U = 0 | Conducteur inférieur U - r2 . i + e2 = 0 U = - e + r . i U = - e + r . (e / r) U = 0 |
Les liaisons G et D sont au même potentiel.
Conséquences
Les conducteurs actifs peuvent être réunis par deux couronnes de forte section, donc de résistance négligeable.
On peut ajouter des conducteurs actifs.
Ainsi à chaque pôle du stator correspondent plusieurs barres (conducteurs) du rotor. De ce fait, même si la f.e.m s'annule dans l'axe interpolaire, les autres conducteurs permettent au couple moteur d'exister.