Le principe
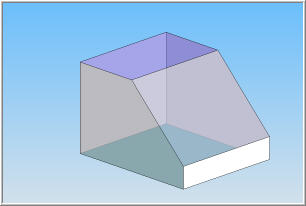			Le principe de la cotation dimensionnelle repose sur l'indication des dimensions portées sur un plan. L'exemple ci-contre d'un prisme à pan coupé montre une vue en perspective de cette pièce. Pour indiquer ces dimensions, le plus simple est de réaliser une vue dans un plan de projection (vue de face, par exemple, et d'y porter  les dimensions caractérisant la pièce).
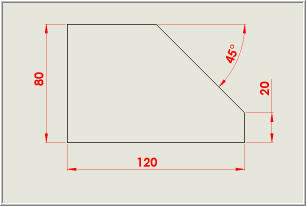			Sur cet extrait de plan, la hauteur du prisme est de 80 mm et correspond à la dimension séparant les deux faces parallèles (bleu et bleu clair). Lorsque la pièce est parfaite (on parle alors de modèle nominal), on peut admettre que cette dimension s'applique entre n'importe quels points des deux surfaces.
Le principe de la cotation, ou du mesurage, dimensionnel repose sur le concept de "bi-points".  Par définition, c'est la longueur d'un segment de droite ou d'un secteur angulaire compris entre deux points appartenant aux deux surfaces à coter.
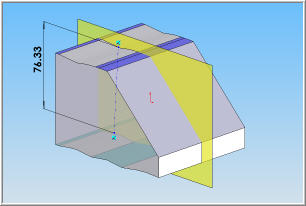			Dans la réalité, les surfaces de la pièce ne sont jamais parfaites (voir illustration ci-dessous, à gauche, qui amplifie les défauts possibles des deux surfaces). Dans ce cas, on peut mesurer en différents endroits les distances entre deux points des deux surfaces. La norme impose que la direction de la mesure (correspondant au segment de droite mesuré) soit définie par l'ensemble des plans parrallèles à celui de la vue cotée.
	L'illustration ci-dessous (gauche) montre que trois mesurages effectués selon 3 directions différentes donnent des résultats différents : Selon la direction D1, les défauts de forme des deux surfaces interviennent sur la valeur de la dimension; Selon la direction D2, c'est l'orientation de la mesure qui intervient sur le résultat; Selon la direction D3, on s'aperçoit qu'il faut imaginer la position du point supérieur et que cela ne facilite pas un mesurage entre deux points "palpables"... L'image de droite montre que l'on peut également retrouver ces défauts de mesurage selon une autre direction...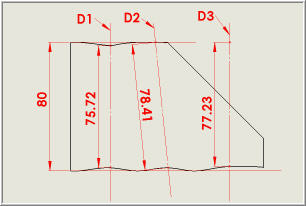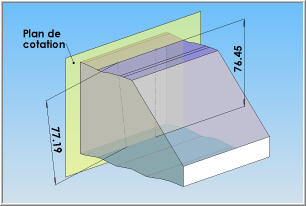
Les cotes
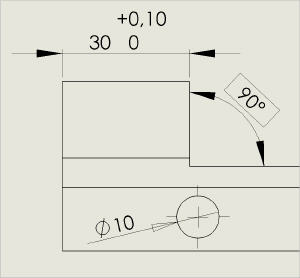			Les cotes permettent d'indiquer des dimensions entre des points, des arêtes et des surfaces d'une pièce. Elles correspondent à la grandeur d'une ligne, d'un angle, d'une épaisseur de matière, d'un diamètre ou d'un rayon d'arbre ou d'alésage. En mécanique, l'unité d'une cote est "implicite" et n'est jamais indiquée. Toutes les dimensions sans unité précisée s'expriment en millimètre (mm, qui correspond à un millième de mètre). Si une cote n'est pas en mm, l'unité doit être précisée (degré pour un angle, par exemple).
	L'extrait d'un plan coté présenté ci-dessus montre des types de cotes classiques utilisées en mécanique

La valeur d'une cote et sa mesure
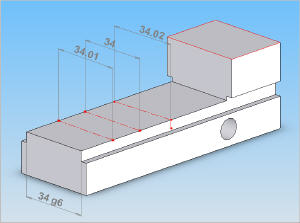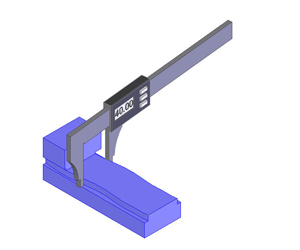
			Dans l'exemple ci-contre, chaque cote correspond à la mesure d'un "bi-points". Mathématiquement, un bipoint est un ensemble de deux points distant d'une grandeur donnée. Mesurer la valeur d'un  bi-point revient à mesurer la longueue du segment de droite reliant ces deux points. En général, chaque point appartient à une surface et l'on estime que la mesure du bi-point correspondra à la distance séparant les deux surfaces. Un difficulté apparaît alors : comment choisir les deux points, ou comment choisir la direction du segment de droite correspondant au bi-point. La figure ci-contre montre que l'on peut obtenir des grandeurs  différentes en fonction de chaque bi-point mesuré. Dans cette illustration, la cote "34 g6" exprime la cote cible attendue et voulue par le concepteur et correspond à un codage particulier (voir Ajustements). Ces variations de grandeur mesurée peuvent être dues à des variations de dimensions de la pièce (erreur de méthode), mais aussi à des erreurs de l'instrument lui-même.
	L'image ci-dessus fait bien apparaître qu'en utilisant un calibre à mâchoire, une simple variation de la position des becs sur une petite surface peut entraîner des résultats différents... ce qui remet en cause ce moyen de mesure dans cette situation.

Les limites de la cotation dimensionnelle

On comprend alors que le contrôle dimensionnel simple par bi-points ne suffise pas dans certains cas et qu'il faille également contraindre la forme des surfaces à respecter certaines conditions géométriques (de forme et d'orientation, par exemple).

Cette considération a amené les techniciens à définir  une exigence dimensionnelle : l'exigence de l'enveloppe.