| Le concept d'intervalle de tolérance | Une dimension réelle parfaitement juste, exacte au sens mathématique, n'existe pas... Chaque dimension réalisée est relative et se situe plus ou moins prés d'un objectif idéal à atteindre, comme une cote moyenne, par exemple. L'exemple ci-dessous montre la schématisation de la mise à longueur d'un axe usiné en tournage (en exagérant les défauts). | | 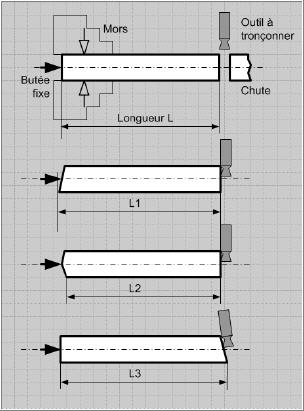 | | Chaque pièce est positionnée et serrée dans un mors et un outil à tronçonner effectue la mise à longueur. Le processus étant stabilisé, on pourrait s'attendre à ce que les longueurs de chaque pièce soient strictement identiques. Or, en les contrôlant, le technicien d'usinage constate qu'il n'en n'est rien. Chaque pièce a une longueur différente. Ces écarts de dimension s'expliquent par des défauts de mise en position sur la butée axiale et par des déformations, même faibles, de l'outil ou de la pièce. Ce constat montre qu'il faut définir un intervalle de longueur dans lequel le technicien considérera qu'une pièce est bonne et lui permettra d'éliminer les pièces dont la dimension de longueur est à l'extérieur de cet intervalle. | | 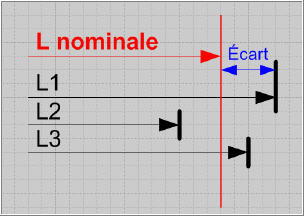 | | Chaque dimension de longueur L possède un écart entre ce qui est mesuré par le technicien et la cote nominale juste qui est recherchée. Cet écart peut être positif (la cote réelle est plus grande) ou négative (la cote réelle est plus petite). Le schéma ci-contre montre les positions de chaque dimension L1, L2 et L3 ainsi que chaque écart par rapport à la cote nominale. | | L'intervalle de tolérance associé à la cote L correspondra à la formalisation d'un écart supérieur et d'un écart inférieur de part et d'autre de la cote nominale. Ces deux écarts forment un intervalle de tolérance qui est égal à leur somme. | | 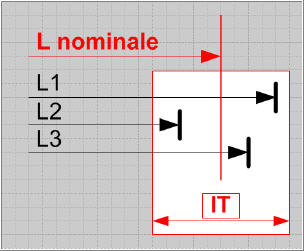 | | 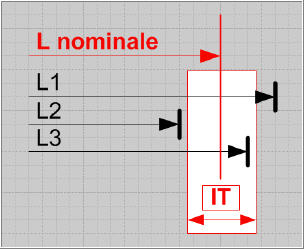 | | 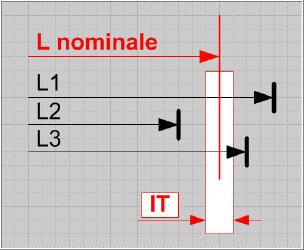 | | La relation suivante permet de calculer la valeur d'un IT Valeur de l'IT = Ecart supérieur - Ecart inférieur Les 3 schémas ci-contre et ci-dessus montrent l'évolution d'un intervalle de tolérance. Lorsque cet intervalle est important, les 3 dimensions L sont considérées comme bonnes. Dans le cas ci-dessus, le technicien doit éliminer les pièces de longueur L1 et L2. dans le cas de gauche, aucune pièce ne serait déclarée correcte si l'IT se réduit encore. | | L'intervalle de tolérance associé à une cote peut prendre différentes "positions" de part et d'autre de la cote nominale. | | 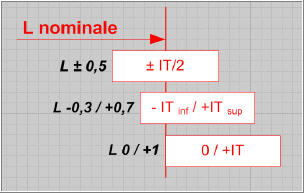 | | Le schéma ci-contre montre 3 positions caractérisques d'un IT: - IT centré de part et d'autre de la cote nominale, les écarts supérieurs et inférieurs sont égaux en valeur absolue;
- IT décentré, les écarts supérieurs et inférieurs étant différents;
- IT en position limite, un des deux écarts est alors nul.
|
Cotation par dimension et intervalles de tolérance Sauf dans certains cas particuliers, chaque cote est donc complétée par un intervalle de tolérance qui définit une zone à laquelle doit appartenir sa grandeur. | | 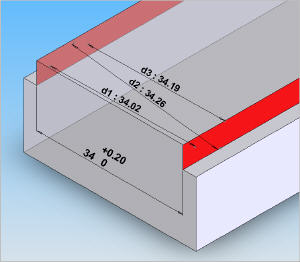
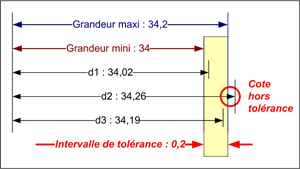
| | Sur l'illustration ci-contre, la cote 34 (0 ; +0,2) définissant la largeur du tenon sur l'embase de l'étau veut dire que la dimension sera acceptée entre les deux bornes 34 - 0 = 34 inclue et 34+0,2 = 34,2 inclue. Cela veut dire que tout bi-point mesuré dans la direction de la cote doit avoir une grandeur comprise entre ces deux limites. Le problème est donc de choisir la bonne direction de mesure et de retenir des bi-points correspondants. La figure ci-contre montre comment 3 bi-points différents peuvent donner des mesures différentes. Lorsque le moyen de mesure devient très précis, la moindre variation de position des points de mesure autour de la direction idéale induit des variations qui peuvent engendrer de mauvaises interprétations de la réalité. | | En effet, selon l'orientation de la mesure, une pièce "bonne" peut être considérée comme "mauvaise", et une pièce "mauvaise" peut être considérée comme "bonne". Cela explique pourquoi il faut toujours effectuer plusieurs mesures lors d'un contrôle manuel entre des points, ce qui permet de limiter l'influence des valeurs aberrantes correspondant à des défauts de mesurages. | | Cette difficulté liée à la cotation dimensionnelle a conduit les organismes de normalisation à développer un concept plus robuste, la tolérancement géométrique par zone de tolérance. |
|