| | 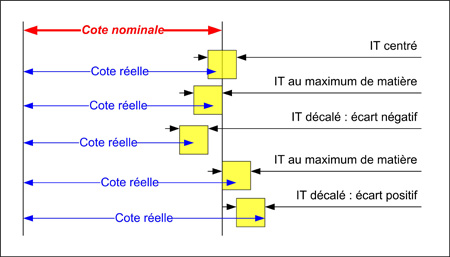
| | La figure ci-contre montre que la position de l'intervalle de tolérance par rapport à la cote nominale influence la grandeur de la cote réelle. |
| Ce schéma fait apparaître la notion d'écart, qui correspond, pour les ajustements, à la distance laissée entre la cote nominale et l'intervalle de tolérance. Cet écart peut être : |
| 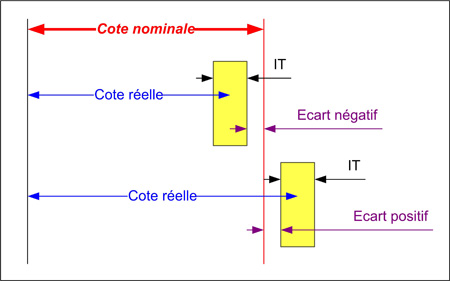
| | nul : une des deux bornes de l'intervalle de tolérance est confondue avec la cote nominale, négatif : l'intervalle de tolérance est décalé vers l'intérieur de la matière et la cote réelle sera toujours plus petite que la cote nominale,
|
| |
| Remarques : il existe un cas particulier très utilisé, celui où l'intervalle de tolérance est également réparti de part et d'autre de la cote nominale (IT centré). dans le cas où l'une des deux bornes de l'intervalle de tolérance est confondu avec la cote nominale (écart nul) on dit que la cotation est au maximum de matière. C'est à dire que la cote nominale correspond alors à la cote maximale possible.
|
| Ecarts supérieurs et inférieurs d'un intervalle de tolérance |
| 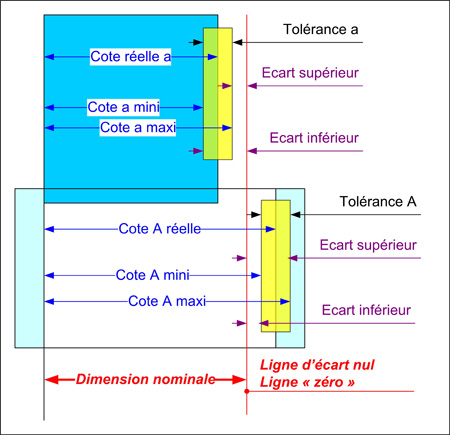 | | Pour définir la position et la grandeur de l'intervalle de tolérance de chacune des deux dimensions constituant un ajustement, il suffit de connaître les écarts supérieurs et inférieurs associés à chaque intervalle et indiquant sa position par rapport à la dimension nominale. La figure ci-contre montre que l'écart supérieur est celui qui correspond à la plus grande dimension et que l'écart inférieur à la plus petite. |
| On peut alors calculer les dimensions maxi et mini des cotes A et a à l'aide des relations suivantes : - A maxi = Dnominal + écart supérieur et A mini = Dnominal + écart inférieur
et - a maxi = Dominal - écart supérieur et a mini = Dnominal - écart inférieur
|