Le concept de droite des moindres carrés permet de bien comprendre pourquoi ce critère d'association a été retenu et comment les logiciels de traitement peuvent être programmés.

La droite des moindres carrés En se plaçant dans un plan, on peut rechercher la droite (en vert dans le schéma ci-dessous) qui représentera le mieux possible la forme générale d'une ligne de forme quelconque (en rouge)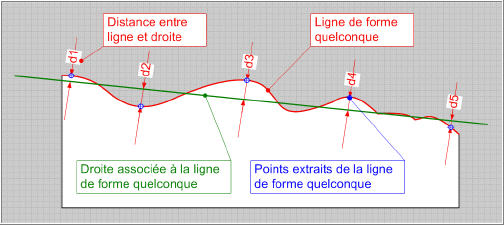
				Pour cela, le concept s'appuie sur chaque point extrait de la ligne quelconque pour déterminer la distance constatée entre chaque point et une droite positionnée de façon quelconque.
Le principe retenu est que la droite verte doit passer entre les points de manière à ce que la somme des distances entre cette droite et les points soit la plus petite possible. Comme les points sont situés de part et d'autre de la droite, certaines distances seront positives et d'autres négatives. Pour annuler l'effet de ce sens, il suffit d'élever au carré chaque distance, ce qui rend le carré de chaque distance toujours positif. Le théorème des moindres carrés dit alors que la droite la plus représentative sera celle dont la position minimise la somme des carrés des distances, d'où le nom de "moindres carrés".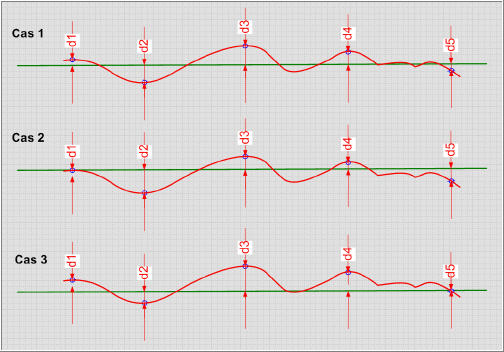
				Le schéma ci-contre montre les résultats du mesurage de 5 points extrait d'une ligne de forme quelconque. Chaque cas proposé correspond à une position particulière de la droite verte. La somme des carrés des distances dans chaque cas peut être calculée simplement dans un tableur...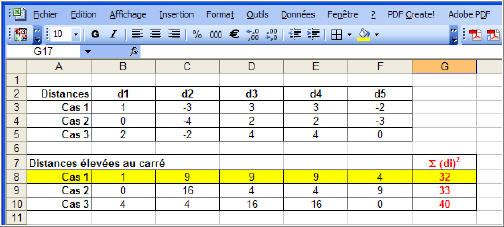
				Le résultat de l'exemple ci-contre montre que c'est le cas 1 qui donne le résultat le plus faible...
Mais cette approche ne permet pas de trouver la position qui minimalise cette somme des carrés et qui correspond à la droite des moindres carrés ce que savent faire certains algorithmes intégrés dans les logiciels de traitement.