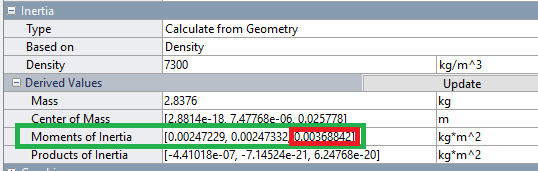
Inertie dans Matlab
L'inertie d'un solide est donnée sous la forme d'une matrice 3 x 3. Cette matrice du tenseur d'inertie est définie ci-dessous à partir des moments d'inertie et produits d'inertie :
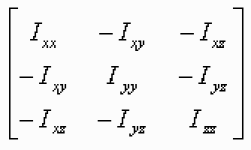
Les moments d'inertie et produits d'inertie sont calculés conformément aux définitions suivantes:
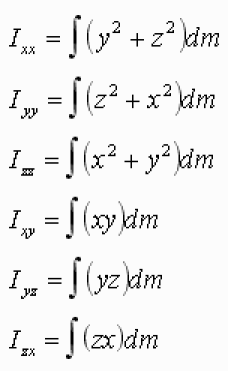
On peut exprimer cette matrice sous la forme suivante :
\(\begin{bmatrix} I_{XX} & -I_{XY} & -I_{XZ} \\ -I_{XY} & I_{YY} & -I_{YX} \\ -I_{XZ} & -I_{YZ} & I_{ZZ}\end{bmatrix}\)
Matlab donne cette matrice sous la forme de deux lignes :
Moments d'inertie : [IXX IYY IZZ] ;
Produits d'inertie : [-IXY -IYZ -IXZ].
Compte tenu de la forme, de l'orientation et de l'axe de rotation du cylindre, c'est la dernière valeur du moment d'inertie qui nous intéresse ici : IZZ.