Etude analytique
Cette partie vise à déterminer les efforts de liaisons dans les articulations en C et D pour lever une personne d'une masse maximale de 110 kg. Cette étude servirait à dimensionner les articulations après une étude en résistance des Matériaux (RdM).
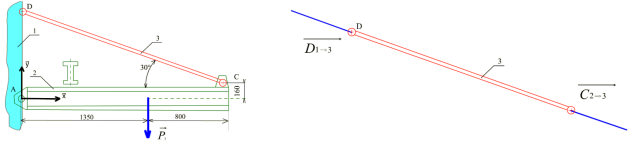
L'étude se fera pour la position du mécanisme définie par le document DR3 - fig.2[1].
On précise que pour cette position la tige du vérin est sortie de 100 mm par rapport à sa position complètement rentrée.
Hypothèses :
Le mécanisme est considéré symétrique dans le plan \((O,\vec{x},\vec{y})\) .
Le poids de toutes les pièces du mécanisme est négligé devant les actions de contact.
Les frottements sont négligés.
Étude de l’équilibre du bras supérieur SE2 = (2)
Fondamental : A retenir : CAS DES SOLIDES SOUMIS A 2 FORCES
Les deux forces \(\overrightarrow{C_{2→3}} \)et \(\overrightarrow{D_{1→3}} \)sont égales et opposées ( \(\overrightarrow{C_{2→3}} + \overrightarrow{D_{1→3}} =\vec{0}\)).
Les forces ont :
même support la droite (CD) (donnée par les deux points d'application des forces) ;
même intensité ;
et des sens opposés.
Ceci permet de déterminer le support des forces mais pas nécessairement l'intensité.
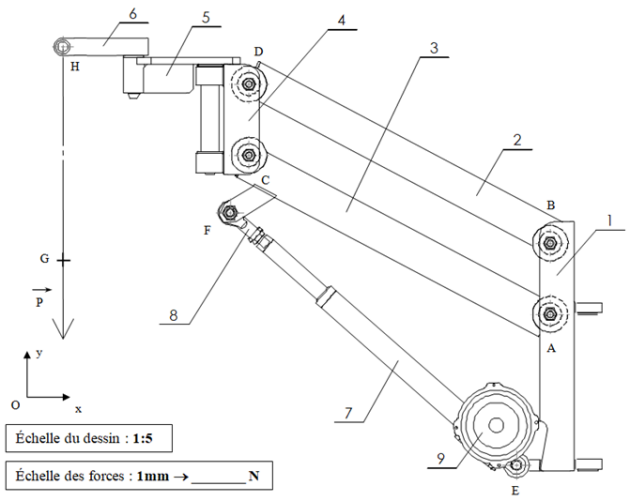
Q8.Justifier que l’action en D de (4) sur (2) notée \(\overrightarrow{D_{4\rightarrow2}}\) a pour support la droite passant par les points B et D. Tracer le support de \(\overrightarrow{D_{4\rightarrow2}}\) sur le DR3-fig1[2].
Q9. A partir d’une figure, justifier l’écriture de l’action mécanique suivantes : \(\{\tau_{4 \rightarrow 2}\}={\begin{matrix} \\ \\ \\ \end{matrix}}_{D} \begin{Bmatrix} -D_{4 \rightarrow 2} \cos(28°) & 0 \\ D_{4 \rightarrow 2} \sin(28°) & 0 \\ 0 & 0\end{Bmatrix}_{(\vec{x}, \vec{y}, \vec{z})}\) avec \(D_{4\rightarrow2}= \|\overrightarrow{D_{4\rightarrow2}}\|\).
Étude de l'équilibre de l'ensemble SE6 = {4, 5, 6, p} avec {p}: la personne soulevée.
Le poids de la personne soulevée est modélisé par le vecteur \(\overrightarrow{P} \)appliqué au point G.
Cette action est définie par le torseur suivant :\( \{\tau_{pesanteur \rightarrow S6}\}={\begin{matrix} \\ \\ \\ \end{matrix}}_{G} \begin{Bmatrix} 0 & 0 \\ -1100 & 0 \\ 0 & 0\end{Bmatrix}_{(\vec{x}, \vec{y}, \vec{z})}\) unités : Newtons
Q10. Établir sur feuille de copie un bilan détaillé des actions mécaniques extérieures s'exerçant sur l'ensemble SE6.
Dans le plan de symétrie \((O,\vec{x},\vec{y})\) de l'ensemble : \(\overrightarrow{CD}\)=(0;100) ; \(\overrightarrow{CH}\)=(-260;152,5) unités : millimètres
Q11. Appliquer le principe fondamental de la statique à l'ensemble SE6 et déterminer \(\|\overrightarrow{C_{SE3→SE6}}\|\). Pour cela, écrire le théorème de la résultante et le théorème du moment au point C.
On rappelle que les trois actions mécaniques peuvent s’écrire de la manière suivante :
\(\{\tau_{2 \rightarrow SE6}\}={\begin{matrix} \\ \\ \\ \end{matrix}}_{D} \begin{Bmatrix} D_{2 \rightarrow SE6} \cos(28°) & 0 \\ -D_{2 \rightarrow SE6} \sin(28) & 0 \\ 0 & 0\end{Bmatrix}_{(\vec{x}, \vec{y}, \vec{z})}\) avec \(D_{4\rightarrow2}= \|\overrightarrow{D_{4\rightarrow2}}\|\) ; \(\{\tau_{SE3 \rightarrow SE6}\}={\begin{matrix} \\ \\ \\ \end{matrix}}_{C} \begin{Bmatrix} X_{C} & 0 \\ Y_{C} & 0 \\ 0 & 0\end{Bmatrix}_{(\vec{x}, \vec{y}, \vec{z})}\) avec \(D_{4\rightarrow2}= \|\overrightarrow{D_{4\rightarrow2}}\|\) et \(\{\tau_{pesanteur \rightarrow S6}\}={\begin{matrix} \\ \\ \\ \end{matrix}}_{H} \begin{Bmatrix} 0 & 0 \\ -1100 & 0 \\ 0 & 0\end{Bmatrix}_{(\vec{x}, \vec{y}, \vec{z})}\)
Q12. Sur DR3-fig2[3], représenter\(\overrightarrow{C_{3→SE6}}\), \(\overrightarrow{D_{2→SE6}}\) et \(\overrightarrow{P}\). Tracer les supports des trois forces. Que remarquez-vous ?
Remarque :
Faire valider par le professeur