Exercice : Estimation d'une masse volumique
On souhaite estimer la masse volumique d'une balle sphèrique. Pour cela, on dispose de la masse et du rayon de la sphère.
masse : \(m=3,4 \pm 0,01\) g (hypothèse d'une loi triangulaire isocèle) ;
Diamètre : \(D=40 \pm 0,1\) mm (hypothèse d'une loi uniforme).
Il n'y a pas de covariances dans cet exemple (donc pas d'étape 5).
Récapitulatif de la procédure d’évaluation et d’expression de l’incertitude
Étape 1 :
Définir le mesurande \(Y\) et la méthode de mesure.
Exprimer mathématiquement la relation entre le mesurande \(Y\) et les grandeurs d’entrée \(X_i\) dont \(Y\) dépend : \(Y = f(X_1,X_2, ...,X_N)\).
La fonction de mesure \(f\) doit contenir chaque grandeur, y compris toutes les corrections et facteurs de correction qui peuvent contribuer à une composante significative de l’incertitude du résultat du mesurage.
Étape 2 :
Déterminer, pour chaque grandeur d’entrée, \(x_i\), la valeur estimée de la grandeur d’entrée \(X_i\), soit sur la base de l’analyse statistique de séries d’observations, soit par d’autres moyens.
Étape 3 :
Estimer ponctuellement la valeur \(y\) du mesurande \(Y\) , c’est à dire l’estimation \(y\) du mesurande \(Y\) , à partir de la relation fonctionnelle \(f\) en utilisant pour les grandeurs d’entrée \(X_i\) les estimations ponctuelles \(x_i\) obtenues à l’étape 2.
Étape 4 :
Évaluer l’incertitude-type \(u(x_i)\) de chaque estimation \(x_i\).
Pour une estimation d’entrée obtenue par l’analyse statistique de séries d’observations, l’incertitude-type est évaluée par la méthode de Type A.
Pour une estimation d’entrée obtenue par d’autres moyens, l’incertitude-type \(u(x_i)\) est évaluée par la méthode de Type B.
Étape 5 :
Évaluer les covariances associées à toutes les estimations d’entrée qui sont corrélées.
Étape 6 :
Déterminer l’incertitude type composée \(u_c(y)\) du résultat de mesure \(y\) à partir des incertitudes-types et des covariances associées aux estimations d’entrée.
Si le mesurage détermine simultanément plusieurs grandeurs de sortie, calculer leurs covariances.
Étape 7 :
Si une incertitude élargie est donnée avec pour objectif de fournir un intervalle de \(y − U\) à \(y + U\) pour que celui-ci comprenne une fraction élevée de la distribution des valeurs que pourraient être attribuées raisonnablement au mesurande \(Y\) , multiplier l’incertitude type composée \(u_c(y)\) par un facteur d’élargissement \(k\), situé en général dans la plage de 2 à 3, pour obtenir \(U = k × u_c(y)\).
Étape 8 :
Donner dans un rapport le résultat du mesurage \(y\) avec son incertitude-type composée \(u_c(y)\) ou son incertitude élargie \(U\) et utiliser un des modes d’expression recommandés.
Décrire, comment les valeurs de \(y\), de \(u_c(y)\) et de \(U\) ont été obtenues.
Question
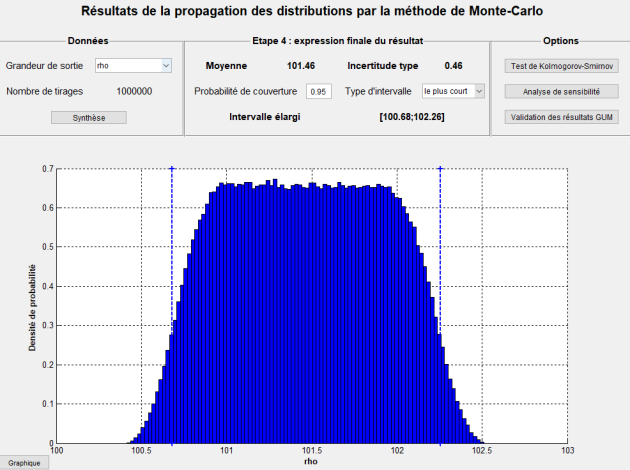
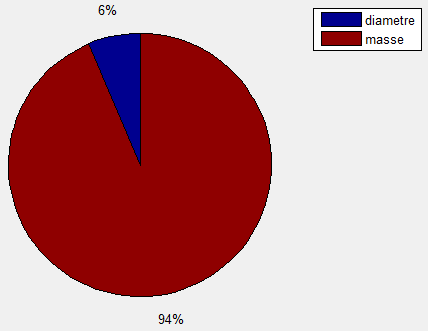
Utiliser le logiciel LNE-MMC pour établir le résultat de mesure de la masse volumique de la balle sphérique.
Question
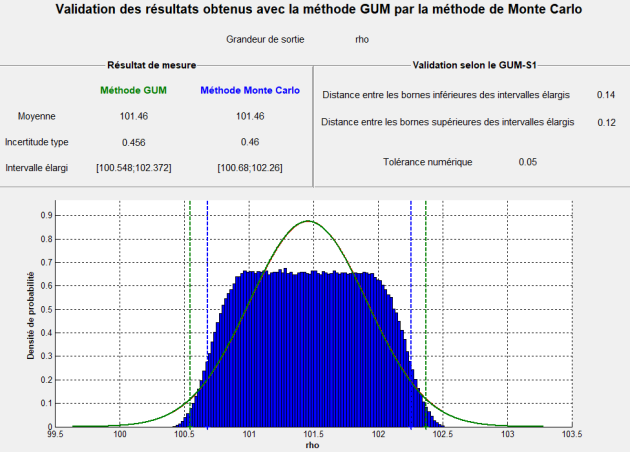
Comparer les résultats obtenus avec la méthode GUM1995 et ceux obtenus avec la méthode de Monte Carlo.