Exercice : Eolienne
Estimation du rendement d'une éolienne par la méthode GUM 1995
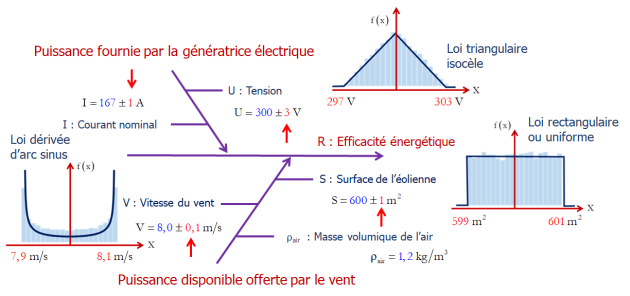
On va s'intéresser, dans cette présentation, à l'estimation de l'efficacité énergétique d'une éolienne. Le mesurande sera noté \(R\) et le modèle de mesure qui permet de décrire la manière dont on va obtenir cette efficacité énergétique fait appel au rapport de 2 grandeurs d'entrée : la puissance fournie par l'éolienne au numérateur de ce rapport et la puissance disponible, c'est-à-dire la puissance offerte par le vent dans une situation donnée.
\(R=\dfrac{\text{Puissance fournie}}{\text{Puissance disponible}}\)
L'expression de \(R\) est transformée en fonction de mesure.
La puissance fournie va être obtenue à partir du produit de la tension par l'intensité (le courant nominal). Au dénominateur vont intervenir la surface de l'éolienne, la vitesse du vent et la masse volumique de l'air.
\(R=\dfrac{U \times I}{\dfrac{1}{2}\rho_{\text{air}} \times S \times V^3}\)
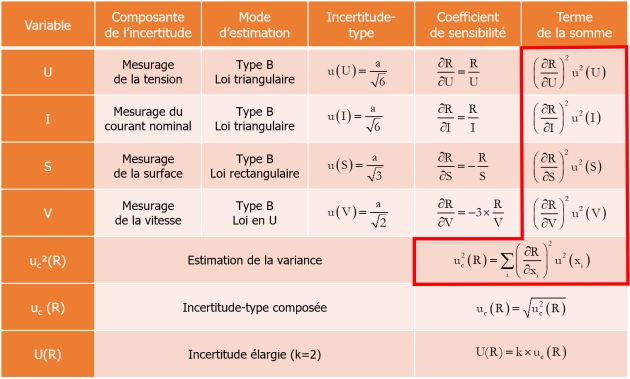
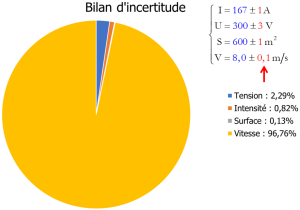
Ces incertitudes qui affectent chacune des grandeurs d'entrée vont se combiner pour se traduire par une incertitude sur le mesurande \(R\). C'est ce qui permettra d'obtenir un résultat de mesure sous la forme d'un intervalle élargi, c'est-à-dire d'un ensemble de valeurs attribuées à l'efficacité énergétique, ici complétée par toute autre information pertinente disponible, comme on va le voir.
\(R^{\textcolor{red}{\pm}}=\dfrac{\textcolor{blue}{U}^{\textcolor{red}{\pm}} \times \textcolor{blue}{I}^{\textcolor{red}{\pm}}}{\dfrac{1}{2} \textcolor{blue}{\rho_{\text{air}}} \times \textcolor{blue}{S}^{\textcolor{red}{\pm}} \times {\textcolor{blue}{V}^{\textcolor{red}{\pm}}}^3}\)
Le résultat de mesure conduit à l'estimation suivante pour l'efficacité énergétique : \(25, 7155\% \leq R \leq28,6464\%\) avec (k = 2).
Le résultat s'accompagne d'un bilan d'incertitude et du diagramme sectoriel ci-contre.
Question
A l'aide du logiciel LNE-MMC, réaliser l'évaluation de l'incertitude du rendement énergétique de l'éolienne.
Question
Comparer les résultats obtenus avec les deux méthodes (GUM 1995 et GUM 2008).