Incertitudes et nombres aléatoires [Méthode Monte Carlo]

Exercice : Incertitudes et nombres aléatoires

Dans cette partie, nous allons voir comment il est possible de générer des nombres pseudo-aléatoires avec python et plus précisément numpy.

En effet, non seulement il est possible de générer des nombres aléatoires, mais il est également possible de les générer de manière à ce qu'ils répondent à une loi souhaitée (normale, uniforme, triangulaire ...).

Pour cela, on utilise les méthodes « random » de la bibliothèque « numpy ».

Question

Exécuter le code suivant.

# -*- coding: utf-8 -*-
### Simulation Monte Carlo ###
### Importation des bibliothèques
import numpy as np
import numpy.random as rd
### Génération des nombres pseudo-aléatoires
x = rd.uniform(-1, 1, 10)
y = rd.normal(-1, 1, 10)
z = rd.triangular(-1, 0, 1, 10)
print (x)
print (y)
print (z)
### Tracé des histogrammes

# -*- coding: utf-8 -*-

### Simulation Monte Carlo ###

### Importation des bibliothèques
import numpy as np
import numpy.random as rd

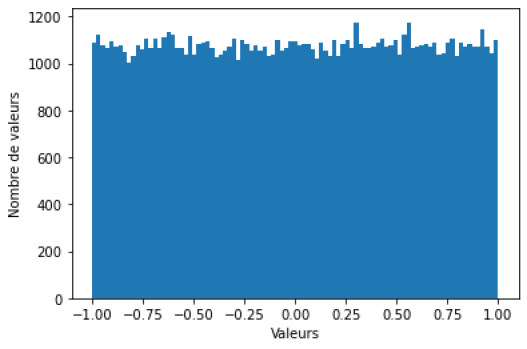
### Génération des nombres pseudo-aléatoires

x = rd.uniform(-1, 1, 10)
y = rd.normal(-1, 1, 10)
z = rd.triangular(-1, 0, 1, 10)

print (x)

print (y)

print (z)

### Tracé des histogrammes

Modifier le code en ajoutant une variable qui gère le nombre de valeurs aléatoires des listes créées.

Question

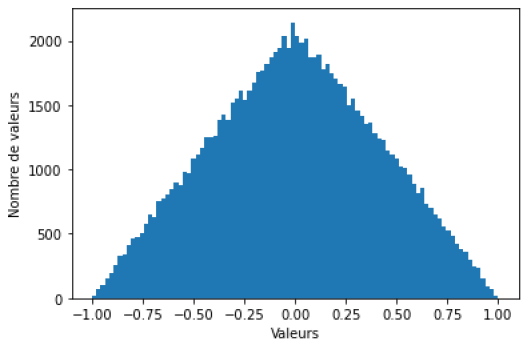
Pour la loi uniforme, tracer l'histogramme montrant la fonction de répartition des valeurs aléatoires.

Indice

Il faut utiliser la bibliothèque matpollit.pyplot.

Indice

Il faut utiliser la méthode « hist » de pyplot.

Solution

Il faut ajouter les lignes suivantes :

### Tracé des histogrammes
plt.figure()
plt.hist (x, range = (-1.5, 1.5), bins= 'rice')
plt.show ()

### Tracé des histogrammes

plt.figure()
plt.hist (x, range = (-1.5, 1.5), bins= 'rice')

plt.show ()

Question

Compléter le code pour générer 100000 nombres aléatoires suivant les 3 lois suivantes.

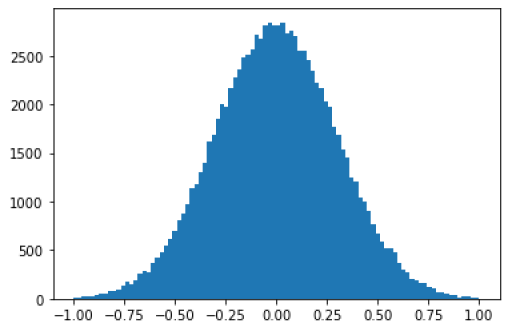
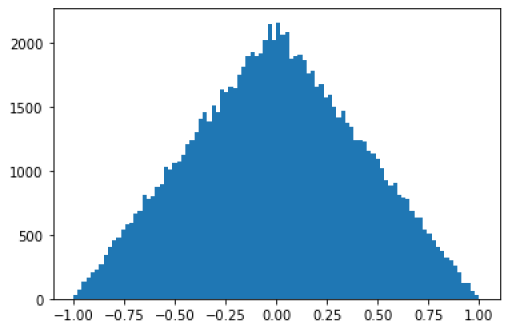
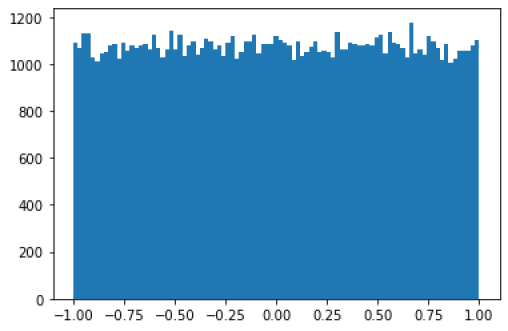
Question

Compléter le code pour afficher les légendes sur les graphiques.

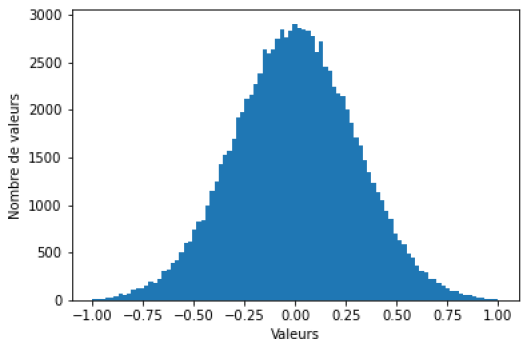
Solution

plt.xlabel('Valeurs')
plt.ylabel('Nombre de valeurs')

plt.xlabel('Valeurs')
plt.ylabel('Nombre de valeurs')

Question

Comparer les incertitudes obtenus par la méthode de Monte Carlo (génération de nombres aléatoires) et les valeurs théoriques.

Indice

Pour afficher la valeur de l'incertitude théorique :

print (1/np.sqrt(3)) # incertitude théorique pour une loi uniforme

print (1/np.sqrt(3)) # incertitude théorique pour une loi uniforme

Indice

Pour afficher la valeur de l'incertitude relative aux valeurs aléatoires :

u_x = np.std(x)		# std pour standard deviation soit écart-type
print ((u_x)) # incertitude par méthode Monte Carlo

u_x = np.std(x)		# std pour standard deviation soit écart-type
print ((u_x)) # incertitude par méthode Monte Carlo

Question

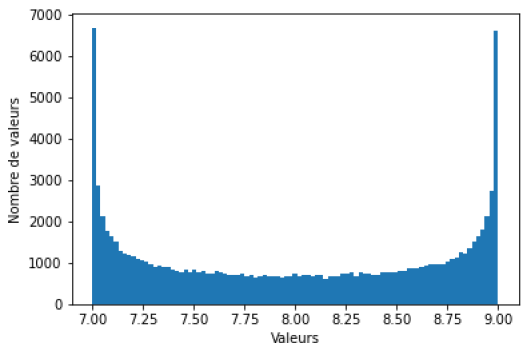
Créer une fonction pour générer une loi dérivée d'arcsin comme dans l'exemple ci-dessous avec \(V=8 \pm 0,1\).