Système Binaire
Définition
Le système binaire est le système de numération utilisant la base 2. On nomme couramment bit (de l'anglais binary digit, soit « chiffre binaire ») les chiffres de la numération binaire. Un bit peut prendre deux valeurs, notées par convention 0 et 1.
Le système binaire est utile pour représenter le fonctionnement de l'électronique numérique utilisée dans les ordinateurs. Il est donc utilisé par les langages de programmation de bas niveau.
Le système binaire le plus courant est la base deux mathématique, permettant de représenter des nombres à l'aide de la numération de position avec seulement deux chiffres : le 0 et le 1.
En base dix, on utilise dix chiffres, de zéro à neuf ; en base n, on utilise n chiffres, de zéro à n – 1 ; donc en base deux on utilise les deux chiffres « 0 » et « 1 ».
Un nombre qui s'exprime en base B par les quatre chiffres 1101 s'analyse 1 × B 3 + 1 × B 2 + 0 × B 1 + 1 × B 0 , qui donne :
1101 en base B = 10 : 1 x 103 + 1 x 102 + 0 x 101 + 1 x 100 = 1 x 1000 + 1 x 100 + 0 x 10 + 1 x 1 = 1101 en base 10 que l'on note : 1101(10) ou (1101)10
1101 en base B = 2 : 1 x 23 + 1 x 22 + 0 x 21 + 1 x 20 = 1 x 8 + 1 x 4 + 0 x 2 + 1 x 1 = 13 en base 2 que l'on note : 13(2) ou (13)2
Exercices de conversion Binaire vers Décimal
Q5. Convertir les nombres binaires suivants en base décimale (base 2 vers base 10) :
1010(2)
1111(2)
1001 0110(2)
1111 1111(2)
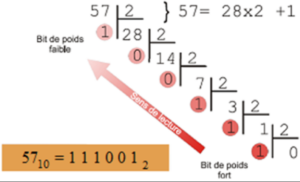
Conversion Décimal vers Binaire par divisions successives (méthode 1)
Pour convertir un nombre décimal en nombre binaire (en base B = 2), il suffit de faire des divisions entières successives par 2 jusqu'à ce que le quotient devienne nul.
Le résultat sera la juxtaposition des restes.
Le bit de poids fort correspondant au reste obtenu à l'ultime étape de la division.
Exemple méthode 1 :
Le nombre décimal N= 57(10) correspond au nombre binaire : 11 1001(2)
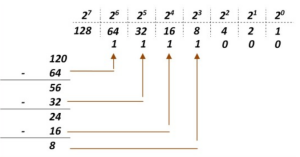
Conversion Décimal vers Binaire par soustractions successives (méthode 2)
Pour trouver le résultat, il suffit :
de trouver le bit de poids fort permettant de s'approcher le plus possible du nombre décimal.
en cas de valeur inférieur, trouver le bit de poids inférieur s'approcher le plus possible du résultat de la soustraction entre la valeur décimale et celle du poids du bit trouvé précédemment.
Exemple méthode 2 :
Le nombre décimal N=120(10) correspond au nombre binaire : 0111 1000(2)
En effet, 120 = 64 + 32 + 16 + 8 + 1
Exercices de conversion Décimal vers Binaire
Q6. Convertir les nombres décimaux suivants en base binaire (base 10 vers base 2) :
19(10)
87(10)
votre année de naissance