Préparation
Travail préparatoire à effectuer hors la classe et à remettre au début de la séance consacrée à cette activité
On considère la figure suivante, destinée à préparer une construction graphique au sein d'une page html dynamique, par le biais d'un script associé.
Un arc de cercle joint les points 1 et 2.
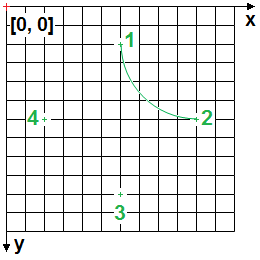
Remarque : Quadrillage et système de coordonnées
Chaque carreau du quadrillage a des côtés de 25 x 25 pixels.
Les coordonnées de chaque point s'écrivent : [x, y] où x est la position en abscisse (position en pixels depuis l'origine, en haut à gauche) et y celle en ordonnée.
Q1 / DÉTERMINER les coordonnées des points 1, ... 4, COMPLÉTER en conséquence le tableau ci-dessous.
Coordonnées | ||
|---|---|---|
Point | x | y |
1 | ||
2 | ||
3 | ||
4 | ||
Q2 / COMPLÉTER (au compas) la figure en opérant successivement deux symétries, l'une par rapport à l'axe vertical médian, l'autre par rapport à l'axe horizontal médian.
Remarque : Figure obtenue
On obtient une sorte d'étoile.
Q3 / DÉTERMINER les coordonnées des centres de chaque arc de cercle nécessaire à la construction. COMPLÉTER en conséquence les deux premières colonnes du tableau ci-dessous.
Coordonnées du centre | Angle (rad) | Rayon (pixels) | |||
|---|---|---|---|---|---|
x | y | début | fin | ||
arc 1-2 | \(\frac{\pi}{2}\) | \(\pi\) | |||
arc 2-3 | 250 | 250 | |||
arc 3-4 | |||||
arc 4-1 | |||||
Q4 / COMPLÉTER le tableau ci-dessus (trois colonnes de droite) : INDIQUER :
l'angle de départ et l'angle de fin pour chaque arc de cercle (en radians)
le rayon de l'arc de cercle (en pixels)
Remarque : Angle
L'angle est compté positivement dans le sens horaire, depuis l'axe horizontal.
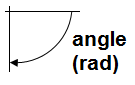
On donne la méthode « canvas » (instruction écrite en « javascript ») permettant le tracé d'un arc de cercle, avec ses paramètres :
context.arc(x, y, Rayon, Angle de départ, Angle de fin) ; |
Paramètre | Description | Unité |
|---|---|---|
x | Coordonnée du centre du cercle, en abscisse | pixel |
y | Coordonnée du centre du cercle, en ordonnée | pixel |
Rayon | Rayon du cercle (en pixels) | pixel |
Angle de départ | angle à partir duquel le tracé de l'arc de cercle débute | radian |
Angle de fin | angle jusqu’au quel le tracé de l'arc de cercle se poursuit | radian |
Q5 / COMPLÉTER le morceau de script ci-dessous, permettant le tracé de l'étoile obtenue à la question 2.
context.arc(250, 50, 100, Math.PI/2, Math.PI) ;
Remarque : Pi
Le nombre \(\pi\) est obtenu avec la méthode « Math.PI ».
Définition : canvas
Zone graphique rectangulaire (transparente) que l'on peut modifier dynamiquement, c'est à dire sur laquelle on peut dessiner, écrire, ... agir via un script (javascript).
Ce type d'élément est pris en charge nativement par le navigateur (Firefox, Internet Explorer, Chrome, ...) et ne nécessite donc pas de plug-in.
Définition : javascript
Langage de programmation de scripts principalement employé dans les pages web interactives.