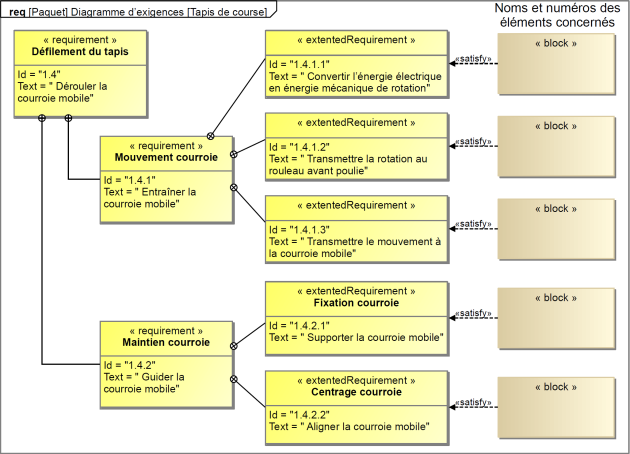
Exercice : Fonction : Dérouler la courroie mobile
L’objectif de cette partie est de valider le choix de la motorisation et de sa commande afin de satisfaire la contrainte du cahier des charges : vitesse allant jusqu’à 19 Km·h-1.
Question
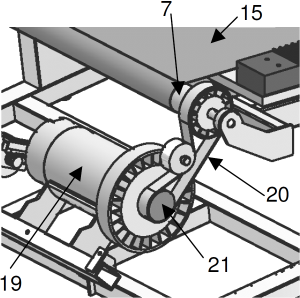
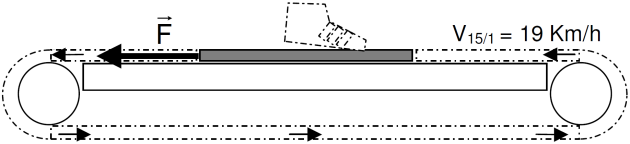
Le cahier des charges impose la vitesse maximale de défilement de la courroie mobile 15 : V15/1 = 19 Km·h-1. On souhaite déterminer la vitesse de rotation maximale du moteur électrique 19 : N19.
Hypothèses :
Le tapis PF790 est réglé à l’horizontale.
La courroie mobile 15 s’enroule sans glisser sur le rouleau avant 7 avec un rendement η1 = 0,95. Le rayon d’enroulement de la courroie mobile 15 sur le rouleau avant 7 est Rr7 = 24,5 mm et le rayon primitif de la poulie du rouleau avant 7 est Rp7 = 44 mm.
L’épaisseur de la courroie mobile 15 est négligée.
Le rendement de la transmission par poulies-courroie (sans glissement) est η2 = 0,95 et le rayon primitif de la poulie moteur 21 est Rp21 = 27 mm.
Question
Déterminer la vitesse de rotation du rouleau avant 7 : ω7 (rd·s-1) puis N7 (tr·min-1).
Indice
La vitesse linéaire : \(\mathbf{v=\omega \times r}\) avec \(\left\lbrace\begin{array}{lll}\text{v : vitesse lineaire }(m\cdot s^{-1})\\\omega \mbox{ : vitesse angulaire }(rad\cdot s^{-1})\\\text{r : rayon (m)} \end{array} \right.\)
Indice
La vitesse angulaire : \(\mathbf{\omega = \frac {2 \times \pi \times N}{60}}\) avec \(\left\lbrace\begin{array}{ll} \omega \text{ : vitesse angulaire }(rad\cdot s^{-1})\\\text{N : frequence de rotation }(tr\cdot min^{-1})\end{array} \right.\)
Question
Calculer le rapport de transmission du système poulies-courroie placé entre le moteur 19 et le rouleau avant 7 : \(\mathbf{\large{r=\frac{N_{7}}{N_{19}}}}\). En déduire la vitesse de rotation N19 du moteur en tr·min-1.
Indice
Le rapport de transmission : \(\mathbf{\large{r=\frac {\text{Diamètre roue menante}}{\text{Diamètre roue menée}}}}\)
Indice
\(\mathbf{{\text{Vitesse de rotation en sortie de réducteur}=\text{vitesse de rotation en entrée} \times \text{rapport de transmission}}}\)
\(\mathbf{{{N_\text{sortie}}=N_\text{entrée} \times r}}\)
Question
Une étude préliminaire du frottement de la courroie mobile 15 sur la plateforme de marche 8 a montré que pour entraîner un coureur de 115 Kg il fallait exercer un effort : F = 230 N. Calculer la puissance mécanique P19 que doit fournir le moteur 19.
Indice
Puissance mécanique de translation : \(\mathbf{P=F \times v}\) avec \(\left\lbrace \begin{array}{lll} \text{P : puissance en Watt (W)} \\\text{F : la force en Newton (N)} \\\text{v : la vitesse linéaire }(m\cdot s^{-1}) \end{array} \right.\)
Indice
Rendement : \(\mathbf{\large{\eta=\frac{P_{\text{sortie}}}{P_{\text{entrée}}}}}\)
Question
Pour la suite, on prendra N19 = 3 400 tr·min-1 comme vitesse de rotation du moteur 19 permettant d’obtenir la vitesse maximale de la courroie mobile 15, et Cu19 = 3,8 N·m, comme couple utile du moteur 19.
On souhaite déterminer la consigne de vitesse du moteur 19 pour qu’il tourne à la vitesse de 3 400 tr/min. (N19)
Question
D’après le DT4, calculer force contre-électromotrice E que produit le moteur lorsqu’il tourne à la cette vitesse.
| DT4 |
Indice
Force contre-électromotrice : \(\mathbf{{E=K_{E} \times \omega}}\) avec \(\left\lbrace \begin{array}{lll} \text{E : force contre-électromotrice (V)} \\K_{E} \text{ : constante de vitesse } (V/rad\cdot s^{-1})\\\omega \text{ : vitesse angulaire } (rad \cdot s^{-1}) \end{array} \right.\)
Question
D’après le DT4, calculer le courant absorbé par le moteur lorsqu’il fournit un couple de 3,8 N·m.
| DT4 |
Indice
Couple : \(\mathbf{{C=K_{T} \times I}}\) avec \(\left\lbrace \begin{array}{lll} \text{C : Couple (N·m)} \\K_{T} \text{ : constante de couple } ( N\cdot m \cdot A^{-1})\\ \text{I : courant moteur (A)} \end{array} \right.\)
Question
D’après le DT4, calculer la valeur de la tension moyenne Um moy à appliquer aux bornes de l’induit du moteur 19 pour obtenir cette vitesse de rotation.
| DT4 |
Indice
Tension moteur : \(\mathbf{{U= E + R\times I}}\) avec \(\left\lbrace \begin{array}{lll|} \text{U : tension moteur (V)} \\ \text{E : force contre-électromotrice (V)} \\ \text{R : résistance d'induit }(\Omega)\\ \text{I : courant moteur (A)} \end{array} \right.\)
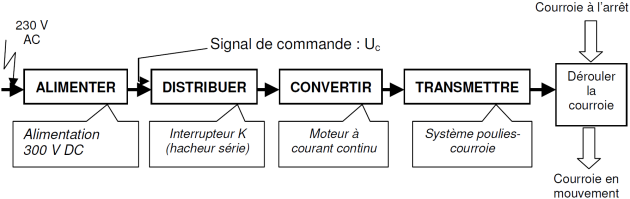
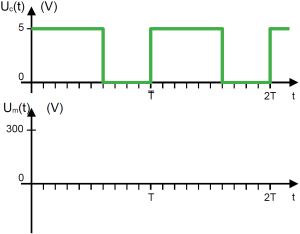
Pour que la fréquence cardiaque du coureur atteigne la valeur souhaitée, la console agit sur la vitesse de défilement de la courroie mobile. Pour cela, elle génère un signal Uc de type MLI (Modulation de la Largeur d’Impulsion) qui est envoyé à la carte variation vitesse, il servira à commander un interrupteur K.
Question
On applique la tension de commande Uc à l’interrupteur K. Compléter ci-contre le chronogramme de la tension aux bornes de l'induit du moteur Um(t).
Question
Calculer la valeur du rapport cyclique α pour obtenir aux bornes de l’induit du moteur la tension moyenne Um moy.
Indice
Tension moyenne d'un hacheur : \(\mathbf{{U_{moy}=\alpha \times U_{max}}}\) avec \(\left\lbrace \begin{array}{lll} U_{moy} \text{ : tension moyenne en sortie du hacheur (V)} \\\alpha \text{ : rapport cyclique}\\ U_{max}\text{ : tension maxi à l'entrée du hacheur (V)} \end{array} \right.\)
Question
Les solutions techniques utilisées pour atteindre la vitesse de 19 km·h-1 (contrainte du cahier des charges) sont-elles adaptées ? Justifier votre réponse.