Moment
Définition : Moment d'une force
Le moment d'une force est l'aptitude d'une force à produire la rotation d'un système autour d'un axe.
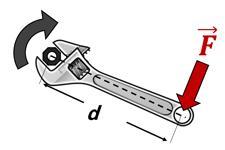
Exemple : Écrou & Clef à molette
Lorsqu'on visse ou dévisse un écrou à l'aide d'une clef, on applique une force sur la clef, ce qui génère une rotation de l'écrou autour de son axe.
Le moment de force dépend de :
la force appliquée sur le bras de levier (F, en Newton) et perpendiculaire à celui-ci
la longueur du bras de levier (d, en mètres).
Seule la composante perpendiculaire de la force appliquée au bras de levier provoque un moment de force.
Le moment de force en Newton par mètre (N.m) s'exprime donc comme suit : \(M_{F}= F\times d\)
Remarque : Signe du moment
Le signe du moment est donné par « le sens de rotation autour du point considéré ». Le signe + correspond au sens trigonométrique.
Remarque : Représentation
Un moment est modélisé par un vecteur lié (qui dépend du point où il est calculé), représenté par une flèche double.
La composante du moment se place sur l'axe perpendiculaire à d et F.
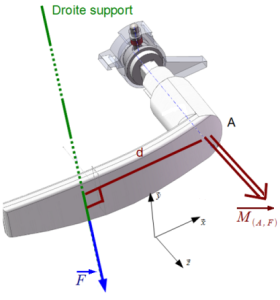
Exemple : Poignée de porte
Le moment, au point A, du à la force \(\overrightarrow{F}\) :
est de signe positif (la force provoque la rotation de la poignée dans le sens trigonométrique)
a une norme \(F \times d\) où \(d\) est la longueur du bras de levier
Le vecteur correspondant est selon \((+)z\) c'est à dire perpendiculaire au plan O(x,y) qui contient \(\overrightarrow{F}\) et \(d\).
On peut écrire :
\(\overrightarrow{M}_{A,\overrightarrow{F}}=\begin{pmatrix}0\\0\\ F \times d\end{pmatrix}\)