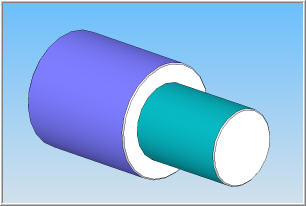
Cette spécification contraint deux surfaces réelles, non idéales (ou non parfaites) a limiter le défaut de coaxialité de chacun de leur axe de symétrie. Les deux axes sont coaxiaux lorsqu'ils sont parfaitement confondus ou alignés.
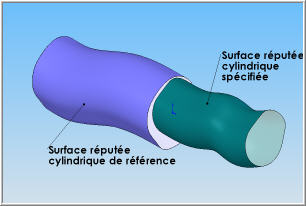
Les deux illustrations ci-dessus montrent un arbre étagé comprenant deux surfaces répuutées cylindriques dont on suppose qu'elles présentent un défaut de coaxialité (illustration de droite).
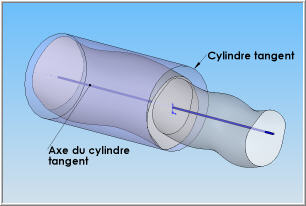
		Pour construire la zone de tolérance qui permettra de fixer les limites de variation de la coaxialité des deux axes, il faut associer un cylindre parfait, tangent du côté libre de la matière et minimisant le défaut d'orientation, à la surface de référence. L'illustration ci-contre montre la construction de ce cylindre et comment on peut en déduire son axe théorique
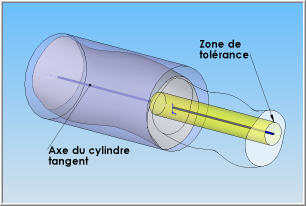
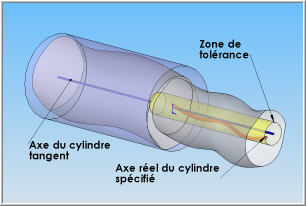
Il devient alors possible de construire une zone de tolérance cylindrique, d'axe confondu avec l'axe théorique du cylindre tangent (en jaune dans l'illustration de gauche ci -dessous).
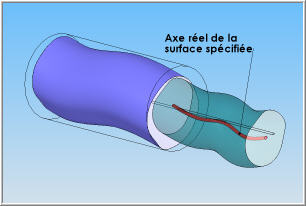
Il est également possible de construire l'axe réel de la surface spécifiée réputée cylindrique (en rouge sur l'illustration ci-dessus à droite).
Pour vérifier la condition de coaxialité des deux axes, il faut vérifier que l'axe réel de la surface spécifiée (en rouge) est entièrement contenu dans la zone de tolérance définie par le cylindre construit sur l'axe théorique du cylindre tangent.