2.9 Simplifications liées aux systèmes plans
Définition d'un système plan
Un système est supposé plan lorsqu'il existe un plan qui soit:
plan de symétrie géométrique
plan de symétrie des actions mécaniques
Exemple 1 : camion vide
Le plan \((O,\vec {x},\vec {y}) \)est plan de symétrie géométrique.
Les actions du sol sur les roues admettent le plan \((O,\vec {x},\vec {y}) \)pour plan de symétrie ( Yavantgauche = Yavantdroit et Yarrièeregauche=Yarrièredroit).
le système est dit "plan".
Exemple 2 : camion chargé d'un côté
Le plan \((O,\vec {x},\vec {y}) \)n'est pas plan de symétrie géométrique.
Les actions du sol sur les roues ne sont plus symétriques ( Yavantgauche < Yavantdroit et Yarrièeregauche<Yarrièredroit).
le système n'est pas plan.
Propriétés utilisables dans un système plan
La résultante est contenu dans le plan (la composante perpendiculaire au plan est nulle).
Le moment est perpendiculaire au plan (les composantes contenues dans le plan sont nulles).
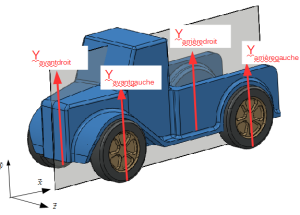
Exemple : Application à l'exemple 1
Dans cet exemple, le système est dit "plan" :\((O,\vec {x},\vec {y}) \)donc :
toutes les composantes des résultantes sur \((\vec {z}) \)sont nulles.
toutes les composantes des moments sur \((\vec {x}) \)et\((\vec {y}) \)sont nulles
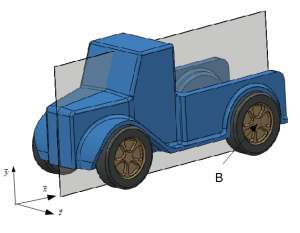
Modélisation de l'action transmissible par le châssis à la roue arrière gauche :
Il s'agit d'une liaison pivot d'axe \((A,\vec {z}) \).
La modélisation de l'action transmissible par la liaison donne :\({T_{chassis \rightarrow Roue}} : \begin{array} {c}\\ \\\\\end{array} _B {\left( \begin{array} {cc}X_{chassis \rightarrow Roue} & L_{chassis \rightarrow Roue}\\Y _{chassis \rightarrow Roue}& M_{chassis \rightarrow Roue}\\ Z_{chassis \rightarrow Roue} &0\\\end{array} \right)}_{(\vec{x},\vec{y},\vec{z})}\)
L'utilisation des propriétés du système plan permet d'écrire :\({T_{chassis \rightarrow Roue}} : \begin{array} {c}\\ \\\\\end{array} _B {\left( \begin{array} {cc}X_{chassis \rightarrow Roue} & 0\\Y _{chassis \rightarrow Roue}& 0\\ 0 &0\\\end{array} \right)}_{(\vec{x},\vec{y},\vec{z})}\)
