Détermination de la vitesse du point G
Schéma cinématique
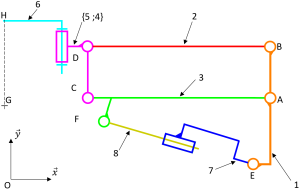
On donne le schéma cinématique du système à parallélogramme en position basse :
Dans ce schéma, le vérin électrique est modélisé par une liaison pivot glissant.
La tige du vérin (8) est complètement rentrée et les bras (2) et (3) sont horizontaux.
Le point F représente le centre de l'articulation entre la tige du vérin (8) et le bras inférieur (3).
La position de la personne est modélisée par le point G qui représente le centre de gravité de la personne à soulever. Ce point est situé sensiblement au niveau des hanches.
On précise que ce point est situé dans le plan de symétrie \((0,\vec x,\vec y)\) de l'ensemble.
La personne est suspendue par un harnais accroché en H et le segment [HG] sera considéré vertical durant tout le mouvement.
Quel que soit le résultat trouvé précédemment, on prendra pour la suite de l'étude : \(\left \|\overrightarrow{V_{F\in3/1}} \right \|= 45 mm.s^{–1}\).
Q8. Mettre en place sur DR2 le vecteur vitesse \(\overrightarrow{V_{F\in3/1}}\) donné à l'échelle demandée.
Q9. Connaissant \(\overrightarrow{V_{F\in3/1}}\), déterminer et tracer \(\overrightarrow{V_{C\in3/1}}\) sur DR2 par la méthode de votre choix. Énoncer sur feuille de copie la propriété utilisée.
Soit l'ensemble S1 = {4, 5, 6, p} avec {p} : personne soulevée.
Q10. Donner la nature du mouvement de l'ensemble S1/1 : Mvt S1/1.
Q11. Justifier l'égalité suivante : \(\overrightarrow{V_{C\in3/1}}=\overrightarrow{V_{C\in S_1/1}}\).
Q12. Sur feuille de copie, rappeler la propriété des vecteurs vitesse des points d'un solide en translation.
En déduire et tracer sur DR2 la vitesse du point G : \(\overrightarrow{V_{G\in S_1/1}}\).
Tracer sa composante verticale et donner sa valeur sur DR2.
Pour la position étudiée, cette vitesse est-elle en conformité avec le CDCF ? (Justifier)