Exercice : Analyse d'un second ordre
Le schéma bloc ci-dessous, montre une version simplifiée de l'asservissement d'un moteur à courant continu.
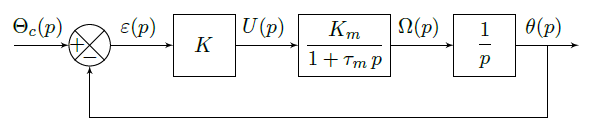
La motorisation est modélisée par la fonction de transfert \(\dfrac{\Omega(p)}{U(p)}=\dfrac{K_m}{1+\tau_m \cdot p}\).
Avec \(K_m=20~rad.s^{-1}.V^{-1}\) et \(\tau_m=0,6~s\).
La tension \(U(p)\) est fournie par un boîtier de commande comportant une partie commande et un module d'amplification. L'ensemble est modélisé par une constante \(K\) dont la valeur est réglable.
\(K = 1 V.rad^{-1}\) est choisi comme valeur initiale.
Un capteur de position assure le retour d'information et est modélisé par un retour unitaire.
Question
Déterminer le temps de réponse à 5% de la motorisation seule.
Question
Quel est le rôle du bloc \(\dfrac{1}{p}=\dfrac{\theta(p)}{\Omega(p)}\)
Question
En appliquant la formule de Black, déterminer la fonction de transfert en boucle fermée de l'asservissement \(\dfrac{\theta(p)} {\theta_c(p)}\). Montrer qu'il s'agit d'une fonction de transfert du second ordre. Puis, identifier le gain statique, la pulsation propre et le facteur d'amortissement en fonction de \(K\), \(K_m\) et \(\tau_m\).
Question
Déterminer si l'asservissement est stable. Puis, par application du théorème de la valeur finale, vérifier que l'asservissement est précis pour une entrée en échelon.
Question
Déterminer le dépassement en pourcentage pour une entrée en échelon ainsi que le temps de réponse à 5% du système.
Question
Vérifier vos résultats à l'aide de Matlab Simulink.
Question
Modifier K pour optimiser le temps de réponse à 5%. Quel est alors le nouveau dépassement ?
Question
Modifier K pour optimiser le temps de réponse à 5% sans dépassement.
Question
Comparer les courbes et vérifier vos résultats à l'aide de Matlab Simulink.