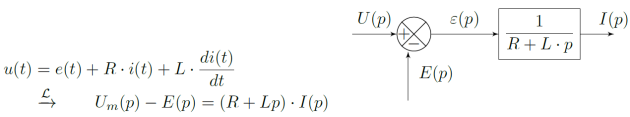Exercice : Le moteur à courant continu
Modéliser un moteur à courant continu (MCC) suppose établir la relation entre sa vitesse de rotation
et la tension appliquée à ses bornes.
Les équations du MCC sont données ci-dessous :
\(u(t)=e(t)+R \cdot i(t)+L \cdot \dfrac{di(t)}{dt}\)
\(e(t)=K_e \cdot \omega_m(t)\)
\(J \cdot \dfrac{d\omega_m(t)}{dt}=C_m(t)-C_r(t)-f \cdot \omega_m(t)\)
\(C_m(t)=K_m \cdot i(t)\)
\(u(t) \)= tension appliquée aux bornes du moteur [V]
\(e (t)\) = force électromotrice [V]
\(i(t)\) = le courant [A]
\(C_m (t) \)= le couple moteur [N.m]
\(C_r (t)\) = le couple résistant [N.m]
\(\omega_m(t)\) = la vitesse de rotation du moteur [rad/s]
\(R\) = la résistance des armatures du moteur [\(\Omega\)]
\(L\) = l’inductance des armatures du moteur [H]
\(J\) = l’inertie du moteur [kg.m²]
\(f\) = coefficient de frottement [N.m.s]
\(K_m\) = constante du couple moteur [N.m/A]
\(K_e\) =constante de force électromotrice [V.s/rad]
Question
Exprimer les transformées de Laplace des équations caractéristiques du moteur, sachant que les conditions initiales sont nulles.
Puis, représenter chacune de ces équations sous forme de schéma-bloc partiel.
Solution
Pour la première équation
On écrit la transformée de Laplace de la première équation et on en déduit le schéma bloc partiel.
Après avoir représenter chacune des équations sous forme de schéma-bloc partiel, on les regroupe afin de représenter le comportement du moteur à courant continu (grandeur d'entrée U(p), grandeur de sortie Ωm(p)).
Question
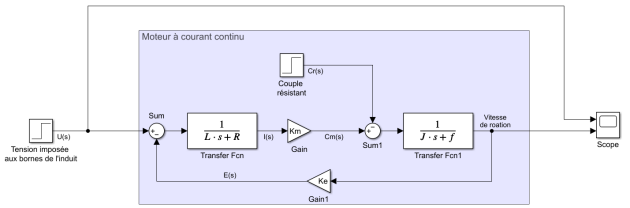
Réaliser le schéma-bloc complet en faisant apparaître les éléments \(U(p),~E(p),~ \Omega_m(p),~ Cm(p),~ Cr(p),~ I(p),~ K_e,~ K_m,~ R,~ L,~ f\) et \(J\).
Question
Modéliser le schéma bloc ci-dessus dans Matlab Simulink.
Solution
Le schéma doit ressembler à ceci :
La tension d'alimentation est de 24 V.
On considère le couple résistant comme nul dans un premier temps.
\(L=2.10^{-3}\) [H]
\(R=2\) [\(\Omega\)]
\(J=5.10^{-2}\) [kg.m²]
\(f=0\) [N.m.s]
\(K_m=K_e=0.8\)
On souhaite effectuer une simulation pendant 3 secondes
Question
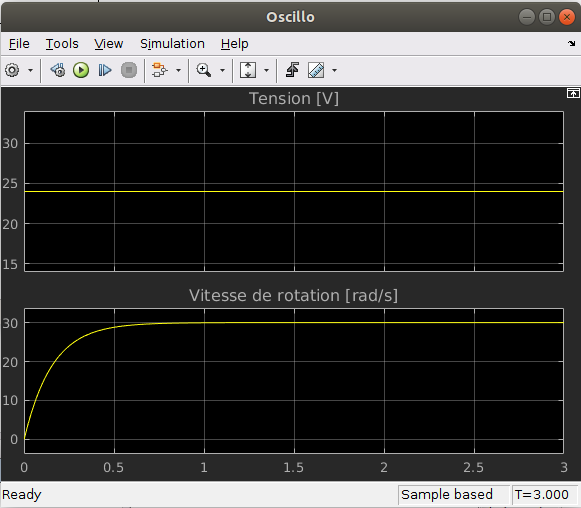
Paramétrer votre modèle Simulink et effectuer une simulation pour visualiser l'évolution de la vitesse de rotation en fonction de la tension d'alimentation.
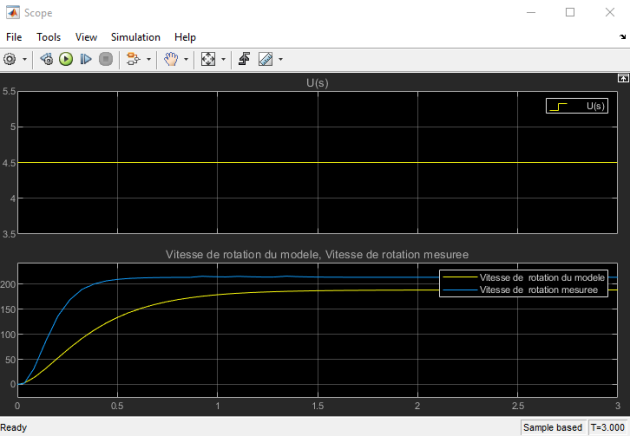
Solution
La réponse du moteur doit ressembler à ceci :
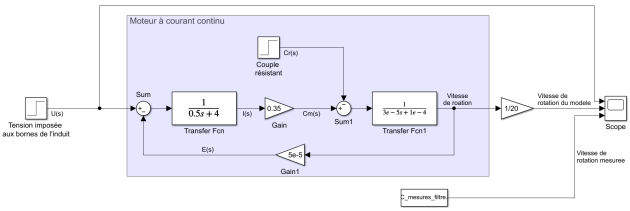
Modélisation du motoréducteur FIT0520
On souhaite modéliser le motoréducteur FIT0520.
Le réducteur sera simulé de manière simple à l’aide d’un bloc « Gain » qui
va multiplier la vitesse de rotation du moteur avec un coefficient 1/20 (le
rapport de réduction).
La troisième voie de l’oscilloscope est connecté à un bloc « from file » (bibliothèque Simulink/Sources), contenant des mesures de vitesse de
rotation du motoréducteur (données dans le fichier ci-dessous).
Fichier contenant des mesures de vitesse de rotation du motoréducteur.
Les autre paramètres du modèle sont les suivants :
La tension d'alimentation est de 4,5 V.
On considère le couple résistant comme nul dans un premier temps.
\(L=0,5\) [H]
\(R=4\) [\(\Omega\)]
\(J=3.10^{-5}\) [kg.m²]
\(f=1.10^{-4}\) [N.m.s]
\(K_m=K_e=0.35\)
Rapport de réduction : \(1/20\)
On souhaite effectuer une simulation pendant 3 secondes
