2. Modélisation dynamique du processus
La question précédente vous a permis de vérifier que la fonction de transfert w=f(u) est une droite. Le système est donc linéaire. Cela veut donc dire que le gain statique reste constant quel que soit le point de fonctionnement.
Pour la modélisation du moteur, nous allons utiliser un modèle du 1er ordre sans retard :
\(\dfrac{\Omega_{moteur}(p)}{U(p)}=\dfrac{K}{1+\tau \, p}\)
Rappel :
Le schéma-bloc du modèle obtenu à partir de l’équation différentielle est :
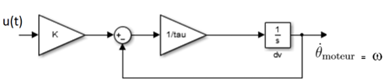
Identification des paramètres dynamiques
On va maintenant estimer finement les paramètres dynamiques (\(K\), \(\tau\)) du système d’entrée \(u(t)\) et de sortie \(\omega(t)\).
Pour cela, vous allez faire un essai de type "réponse à un échelon" sur le système réel mis en parallèle avec le modèle. L’identification sera réalisée lorsque les courbes temporelles des 2 sorties \(\omega(t)\) seront identiques.
Protocole expérimental
Ouvrir maintenant le fichier Simulink Identif_dynamique.slx
Le programme est déjà configuré pour générer une commande en échelon (positif et négatif)
Exécuter le programme (attendre car il y a une compilation et un transfert du code vers la cible).
Modifier en temps réel (sans arrêter le programme) les paramètres K et τ tant que les courbes des 2 sorties ne sont pas superposées.
Réglage de K en premier (superposition valeurs finales)
Ensuite réglage de τ (régime transitoire)
Donner les valeurs obtenues dans le tableau suivant :
K
\(\tau\)
Donner une valeur approximative du temps de réponse à 5%