Modélisation
Modèle d’ordre 1
Ce modèle correspond à une fonction de transfert de la forme : \(G_v(p)=\dfrac{\Delta M_T(p)}{\Delta S_r(p)}=\dfrac{G_{v0}}{1+\tau \, p}\).
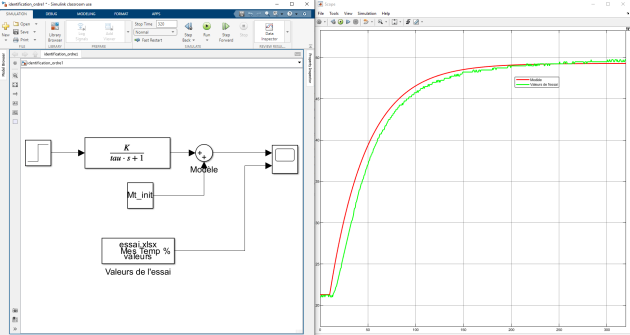
A l'aide de Matlab, réaliser un modèle d'ordre 1 avec la constante de temps trouvée précédemment, le gain identifié et comparer le modèle au relevé enregistré lors de l'expérimentation.
Expliquer pourquoi ce modèle d’ordre 1 n’est pas suffisamment fidèle.
Modèle d’ordre 2 décomposable
Ce modèle correspond à une fonction de transfert de la forme : \(G_v(p)=\dfrac{\Delta M_T(p)}{\Delta S_r(p)}=\dfrac{G_{v0}}{(1+\tau_1 \, p)\,(1+\tau_2 \, p)}\).
Identification
Déterminer par la méthode de Strejc-Broïda les valeurs des constantes de temps \(\tau_1\) et \(\tau_2\).
Comparaison modèle-réel
A l'aide de Matlab, réaliser le modèle d'ordre 2 et comparer le modèle au relevé enregistré lors de l'expérimentation.
