2. Correction proportionnelle intégrale P.I.
Dans les faits, la fonction de transfert est d’ordre 3 : \(G_v(p)=\dfrac{G_{v0}}{(1+\tau_1 \, p)\, (1+\tau_3 \, p) \, (1+\tau_3 \, p)}\) avec \(\tau_1>\tau_2>\tau_3\)
2.1. Prédéterminations
On envisage le système en BF avec un correcteur à action Proportionnelle + Intégrale tel que : \(Sr(t)=k.(\epsilon(t)+\dfrac{1}{T_i} \, \int \epsilon(t) \,dt\) avec \(\epsilon(t)=(C-M_T)\) et \(T_i\) la constante de temps d’intégration.
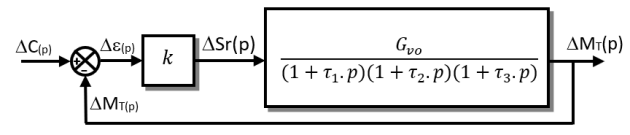
A partir du modèle obtenu d’ordre 3, on envisage donc le schéma-blocs en BF ci-dessous.
On notera : \( k_0=\dfrac{k . G_{v0}}{T_i}\) coefficient global en BO
Q17. Exprimer la fonction de transfert en BO : \(O(p)=\dfrac{\Delta M_T(p)}{\Delta \epsilon (p)}\). Simplifier cette expression si on choisit \(T_i=\tau_1\) (méthode dite de la « compensation du régime dominant »). Puis, exprimer la fonction de transfert en boucle fermée et en variation sous la forme donnée ci-dessous :
\(F(p)=\dfrac{\Delta M_T(p)}{\Delta C(p)}=\dfrac{1}{\Biggl(1+\dfrac{2 \, \xi_F}{\omega_F}p+\dfrac{1}{{\omega_F}^2}p^2 \Biggr) \, (1+\tau_F \, p)}\)
Par identification, en déduire les trois relations qui devraient permettre de résoudre le système. On souhaite un réglage avec un degré de stabilité imposé tel que \(\xi_F=0,5\), résoudre le système d’équations. Valider la valeur calculée avec le modèle Matlab en simulation.
2.2. Expérimentation
Q18. Avec le logiciel, définir \(k_1=1\) et \(k_2=k\) (valeur calculée précédemment), définir \(T_i=\tau\), visualiser la réponse temporelle en régime d’échelon et comparer le résultat obtenu avec celui de la simulation. Vérifier le comportement lors de l’application d’une perturbation.