Modélisation du système bouclé, et détermination des paramètres du correcteur
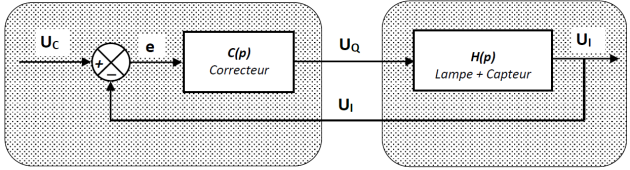
Schéma bloc du système bouclé
L’asservissement global de notre système peut être imagé par le schéma bloc simplifié suivant :
Modélisation du système bouclé, et détermination des paramètres du correcteur
La structure du correcteur géré par l’API est de type « Mixte », et on retiendra par exemple un correcteur de type « PI ».
La fonction de transfert du correcteur s’écrit alors :
\(C(p)=\dfrac{U_Q(t)}{e(t)}=K. \Bigg( 1+\dfrac{1}{\tau_i.p}\Bigg)\)
Q2. Exprimer la fonction de transfert du système bouclé :
\(BF(p)=\dfrac{U_I(t)}{U_C(t)}=\dfrac{N(p)}{D(p)}\)
Soit D(p) le dénominateur de cette fonction de transfert :
Q3. Compte tenu des expressions de et de retenues dans cette application, proposer une écriture du type
«\(p²+2.\xi.p.\omega_n+\omega_n²\)» pour ce dénominateur D(p).
Le résultat doit être :
\(p²+\dfrac{1+G.K}{\tau}.p+\dfrac{G.K}{\tau_i.p}\)
Les pôles sont les racines de ce dénominateur, et dans le domaine temporel, l’identification des paramètres «\(\xi\)» et «\(\omega_n\)» va permettre de connaitre l’allure de la réponse indicielle du système bouclé.
Dans cette application, on souhaite :
Que la réponse temporelle soit la plus rapide possible, mais sans dépassement ;
Que le temps de réponse à 5 % soit de l’ordre de 100 secondes.
D’après les annexes mises à disposition, on en déduit que :
Réponse rapide et sans dépassement \(\rightarrow\) c'est-à-dire que \(\xi=1\) (pôles confondus) ;
Temps de réponse de 100 sec \(\rightarrow\) c'est-à-dire que \(\omega_n\) soit tel que tr = 4,8.Tn = 100 sec (tr = temps de réponse indicielle à 5% pour \(\xi=1\)).
Q4. Compte tenu des informations précédentes relatives à la réponse indicielle attendue, exprimer puis calculer les paramètres du correcteur : K et \(\tau_i\)