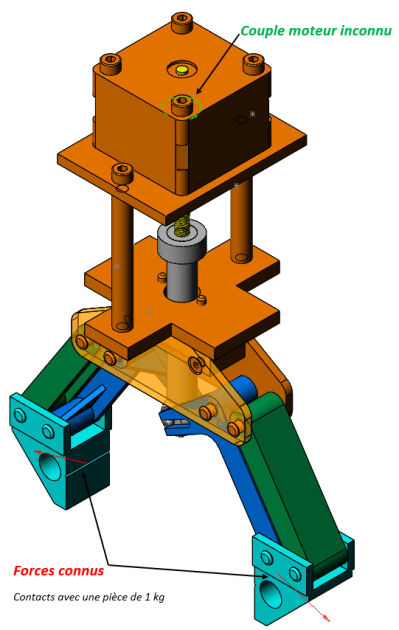
Analyse des efforts exercés par la pince pour soulever la pièce
On désire soulever une pièce de masse m=1kg avec la pince. Deux forces connues ont donc été mises en place sur les mors (voir la maquette numérique). Ces forces symbolisent le contact avec une pièce de masse 1kg.
L'objectif est de vérifier que le moteur utilisé possède un couple suffisant. Pour cela, on utilisera le logiciel de calcul mécanique Méca 3D.
Attention : Actions réciproques
Les forces représentées sous Meca3D sont les forces de la pièce sur les mors gauche et droit.
Il faudra donc penser au principe des actions réciproques quand vous isolerez la pièce à soulever.
Ce principe des actions réciproques constitue la troisième loi de Newton : « Tout corps A exerçant une force sur un corps B subit une force d'intensité égale, de même direction mais de sens opposé, exercée par le corps B ».
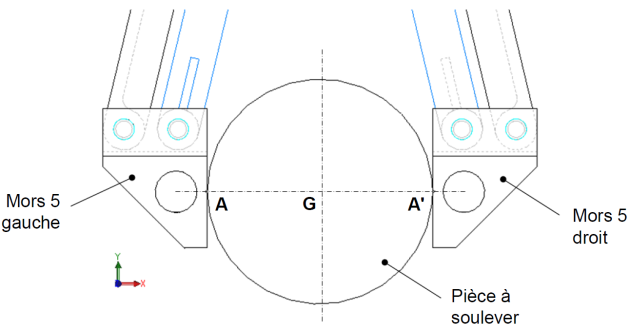
Le schéma du dispositif de préhension de la pièce à soulever est le suivant :
On isole la pièce à soulever.
La pièce à soulever à une masse maximale de 1kg.
On considère le problème plan.
Q6. Sachant que l'accélération de la pesanteur est égale à g=10m/s², calculer la norme du vecteur poids de la pièce à soulever et noter ses composantes, dans le repère (G, \(\vec{x}\), \(\vec{y}\), \(\vec{z}\))
Norme | Composantes |
|---|---|
\(\|{\overrightarrow{P_{piece}}}\|\) | \(\overrightarrow{P_{piece}}=\begin{pmatrix} ... \\ ... \\ ... \end{pmatrix}\) |
Q7. Avec le logiciel de calcul, relever les composantes des forces exercées sur la pièce à soulever par les mors 5 (ces forces sont déjà définies dans Meca3D). Justifier la valeur des composantes en \(\vec{y}\) (effort tangentiel) des forces exercées par les mors 5 sur la pièce à soulever.
Mors gauche | Mors droite |
|---|---|
\(\overrightarrow{F_{5→piece}}=\begin{pmatrix} ... \\ ... \\ ... \end{pmatrix}\) | \(\overrightarrow{F'_{5→piece}}=\begin{pmatrix} ... \\ ... \\ ... \end{pmatrix}\) |
Afin d'éviter le glissement de la pièce, on se place à la limite de l'adhérence.
Les mors sont en polyamide et la pièce à soulever en acier.
Q8. D'après le tableau des valeurs du facteur d'adhérence [pdf], en déduire le facteur d'adhérence limite (on se place dans le cas le plus défavorable). Vérifier que le facteur d'adhérence est supérieur à 0,3 et que l'angle limite d'adhérence est supérieur à 17°. Justifier alors qu'il y aura bien adhérence de la pièce à soulever par rapport au mors et tracer les trois forces (\({\overrightarrow{P_{piece}}}\), \(\overrightarrow{F_{5→piece}}\), \(\overrightarrow{F'_{5→piece}}\))sur le schéma (échelle : 1 cm ≡ 5 N).