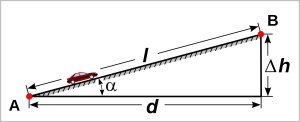
Étude de la course du vérin
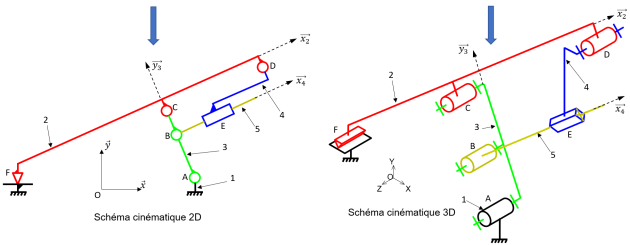
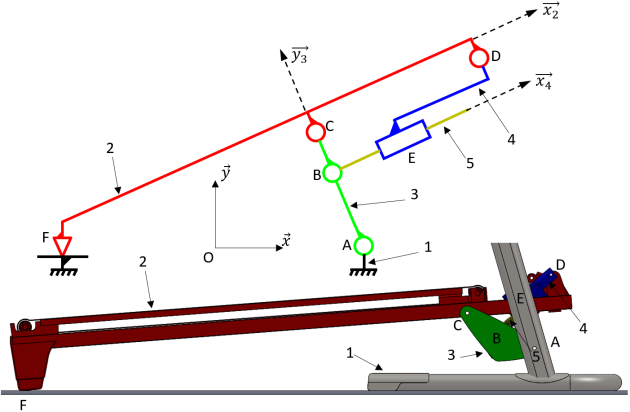
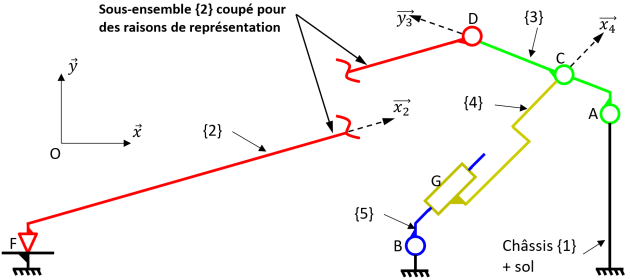
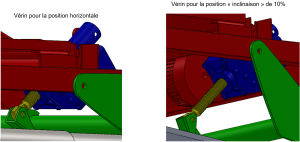
Il s'agit des schémas cinématiques de la chaîne de puissance de l'inclinaison du tapis. La solution présentée est simplifiée car elle ne fait apparaître qu'une liaison glissière (pour représenter le vérin électrique) et ne montre pas le mécanisme complet (réducteur + vis-écrou) qui permet d'obtenir le déplacement de la tige (solide repéré 5).
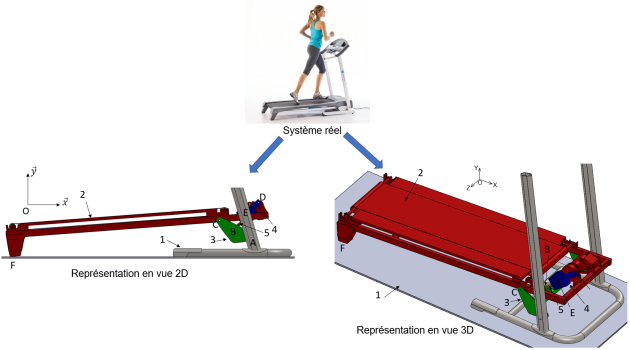
Il existe différentes versions du tapis comme ci-dessous.
Q7. Quel est le nom de la liaison au point G et au point D et au point C ?
On donne une maquette numérique simplifiée pour mettre en œuvre le mécanisme d'inclinaison.
Ci-contre, on peut voir le tapis dans les deux positions extrêmes.
Ci-contre, on peut voir le tapis dans les deux positions extrêmes.
Vous remarquez qu'entre les deux positions la tige du vérin s'est déplacée.
Ainsi, la longueur du vérin (entraxe) est la suivante pour les deux positions :
En position rentrée : 203,48 mm
En position sortie : 270,15 mm
Q8. En déduire la course du vérin (valeur entière approchée) en mm.
Téléverser le dossier zippé sur le bureau et en extraire tout le contenu (cliquer droit sur le dossier et opter pour Extraire tout...). En fin de séance, effacer les DEUX dossiers (dossier zippé et dossier ordinaire).
Avec le logiciel SolidWorks, ouvrir le fichier de type assemblage "Tapis TC290 Meca3D.SLDASM".
Ce fichier contient le mécanisme complet. Activer le complément Méca3D[1]
Cliquer droit sur "Analyse" et sélectionner "Calcul mécanique".
Une fenêtre s'affiche donnant des informations sur le mécanisme (nombre de cycles, hyperstatisme, nombre d'équations...).
Cliquer sur "Continuer".
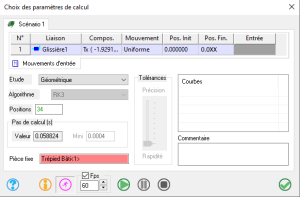
Pour vérifier le bon fonctionnement dans un premier temps, faire une étude géométrique, pour 34 positions, avec la translation TX de la liaison glissière comme mouvement d'entrée pour la valeur de la course calculée précédemment "XX" mm.
Valider le paramétrage en lançant un calcul (flèche verte)
à ne pas confondre avec la coche verte qui permet de sortir de la fenêtre
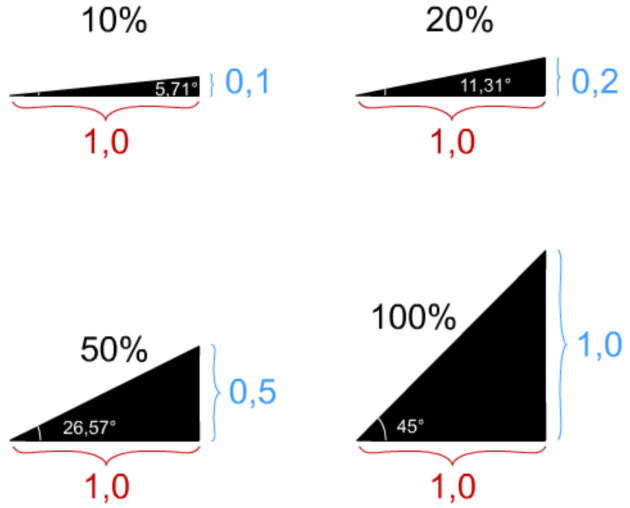
Il faut maintenant récupérer les résultats pour visualiser qu'une course du vérin de XX mm permet bien d'avoir une inclinaison de 10 %.
Q9. Relever la valeur de la position en rotation pour la liaison "Linéaire rectiligne1". Justifier que le cahier des charges est satisfait, vis à vis de l'inclinaison maximale de 10% .
Complément : Pente en pourcent
Schéma en coupe longitudinale d'un tronçon routier rectiligne :
\(d\) = distance horizontale
\(\Delta h\) = différence de hauteurs, d'altitudes = dénivelé
\(\alpha\) = inclinaison, angle d'élévation
pente = \(\tan(\alpha) = \frac{\Delta h}{d}\)
\(l\) = longueur suivant la pente.
