Prise en compte de l'inclinaison pour l'action de la pesanteur
Simulation et résultats du montage 1 en position inclinée avec la pesanteur
Ouvrir le modèle "Montage1_trans".
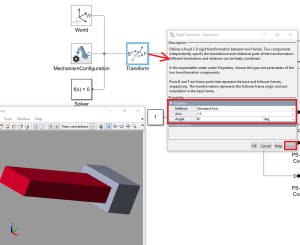
Double-cliquer sur le bloc "Transform".
Développer la ligne "Rotation" (en cliquant sur le "+").
Sélectionner "Standard Axis" pour la méthode, "+X" comme axe de rotation et "60°" comme angle de rotation.
Cliquer sur "Apply" puis sur "OK".
Dans la fenêtre Simulink, cliquer sur "Simulation" → "Update diagram" (ou appuyer sur "CTRL + D").
Supprimer l'effort moteur (le mettre à 0).
Laisser l'action de la pesanteur.
Réaliser une simulation pendant 3 secondes.
Lancer la simulation.
Que se passe-t-il ?
Comparer la valeur de l'accélération en mm.s–2 subit par le parallélépipède avec la valeur de l'accélération de la pesanteur et le cosinus de l'angle de 60°.
Mettre en place l'action de la pesanteur sur la figure et écrire les composantes du poids dans le repère R0 et R1 .
Justifier le comportement et les résultats (en particulier la valeur de l'accélération du mouvement).
Faire valider par le professeur.
Fondamental : Travailler dans un repère incliné
Il est souvent plus judicieux de travailler dans le repère inclinée car la majorité des forces sont exprimées dans ce repère et que seule l'action de la pesanteur est verticale par exemple.
Vous rencontrerez de nombreux exercices dans ce cas de figure.
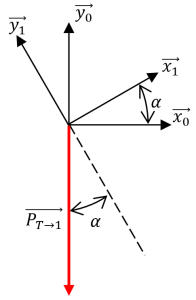
Dans ce cas, il est important de savoir repérer l'angle d'inclinaison, ici l'angle α (entre X0 et X1) ET d'être capable de retrouver l'angle entre la verticale l'axe Y1.
Il ne faut pas hésiter à faire une figure pour bien positionner les angles.
Dans la figure ci contre, on remarque que :
\(\overrightarrow{P_{T→1}} = -P_{T→1} . \vec{y_0} =-M_1 . g . \vec{y_0} = -M_1 . g . (sin(\alpha)\vec{x_1}+cos(\alpha)\vec{y_1})\)
En modélisant le mécanisme et en écrivant l'équation de la résultante du principe fondamental de la dynamique en projection sur l'axe Y1, quelle force faut-il appliquer pour que le parallélépipède se déplace suivant l'axe Y1 vers le haut avec une accélération de 0,25 m.–2 pendant une seconde.
Avec le logiciel, appliquer cette force et faire valider par le professeur.
Compléter le document réponse.