Régulation de température d’air

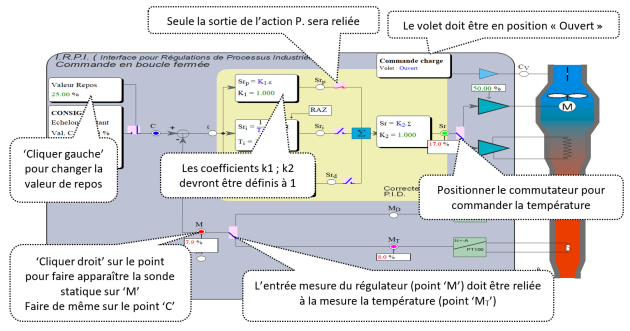
a. Choisir le mode de commande "En boucle fermée avec correcteur PID". Pour cela "cliquer" sur les menus successifs : Choisir → Mode de commande → Boucle Fermée → PID

b. Connecter la sortie régulateur, repérée 'Sr', à la commande débit. Pour cela "cliquer" dans la zone repérée au-dessus du commutateur.

c. Positionner une sonde de mesure sur la mesure température repérée "M_T" : pour cela "cliquer droit" dans la zone circulaire dessus point M_T.

d. Faire de même pour le point de mesure repéré Sr

e. Régler la commande indépendante du débit à 50%

f. Définir \(k_1\)et \(k_2\) (cela permet d’avoir une boucle fermée sans correction)

g. Fermer le contacteur de l’action P (Srp), relié au sommateur

h. Relier la mesure de température M_T à l’entrée de la mesure du régulateur M (dans la boucle de retour) en positionnant le commutateur correctement.

i. Faire de même pour le point de consigne repéré C

Q9. Pour différentes valeurs de repos, comprise entre 30 et 70%, par pas de 10%, relever après stabilisation la mesure de la température, la valeur affichée au point M_T. Pour changer la valeur de repos il suffit de "cliquer" dans le bloc repérée "Valeur de repos" et d'introduire une nouvelle valeur. Remplir le tableau de mesure :

Q10. Tracer la caractéristique statique M_T = fn(C) (avec le logiciel « Excel » par exemple). Monter que cette caractéristique est sensiblement linéaire. Faire afficher l’équation de la courbe de tendance. Définir la valeur de commande de repos notée \(C_0\) qui permettra d’obtenir une mesure de repos notée \(M_{T0}\) de valeur la plus proche possible de 50%. En déduire la valeur du coefficient de transfert statique en BF défini par : \(G_{BF0}=\dfrac{M_{T0}}{C_0}\). En déduire la valeur du coefficient de transfert en variation autour du point de repos : \(G_{BFv}=\dfrac{\Delta M_T}{\Delta C}\)