2. Etude en régime d'échelon constant
2.1. Relevé de la réponse temporelle
2.1.1. Expérimentation
On souhaite relever la réponse temporelle suite à une variation de la commande ±20% autour du point repos.
Effectuer dans l’ordre indiqué :
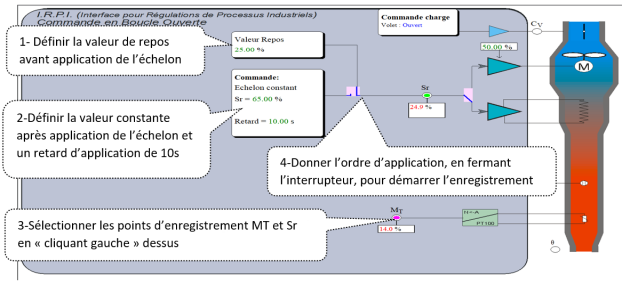
Définir la valeur de repos avant application de l’échelon ;
Définir la valeur constante après application de l’échelon et un retard d’application de 10s ;
Sélectionner les points d’enregistrement MT et Sr en « cliquant gauche » dessus ;
Donner l’ordre d’application, ce qui aura pour effet de démarrer l’enregistrement.
Visualiser la réponse temporelle en "cliquant" sur le bouton
On peut ‘cliquer’ sur le bouton
pour obtenir des explications sur la façon de procéder.Adapter les échelles en X, grâce au bouton
et en Y, grâce au bouton 
afin que la partie intéressante de la courbe occupe l'ensemble de l'écran.
2.1.2. Exploitation
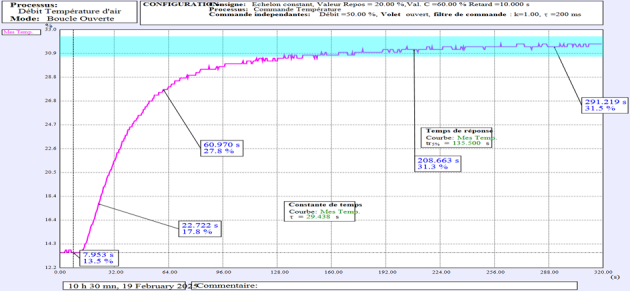
Q4. Déterminer la constante de temps dominante en "cliquant" sur le bouton 
et en positionnant les sondes demandées. ‘Cliquer’ sur bouton 
pour explications éventuelles. Déterminer le temps de réponse à 5% noté tr5% en "cliquant" sur le bouton 
et en positionnant les sondes demandées. ‘Cliquer’ sur bouton pour explications éventuelles. Inscrire en zone commentaire vos noms et groupe de TP. Justifier, à partir de la réponse expérimentale obtenue et de ses exploitations, que le processus étudié n’est pas parfaitement d’ordre 1. Faire un "copier Ctr/C - coller CTR/V" dans un document "Word" pour votre compte rendu personnel.
Afin d’exploiter ultérieurement ce relevé expérimental, effectuer des enregistrements sous les différents formats proposés :
‘Fichier’ puis ‘Enregistre sous…’ pour un enregistrement de type *.reg
‘Fichier’ puis 'Exporter…’ pour un enregistrement de type *.txt
‘Fichier’ puis ‘Exporter Xml…’ pour un enregistrement de type *.xml
2.2. Modélisation
2.2.1. Modèle d’ordre 1
Ce modèle correspond à une fonction de transfert de la forme : \(G_v(p)=\dfrac{\Delta M_T(p)}{\Delta S_r(p)}=\dfrac{G_{v0}}{1+\tau \, p}\).
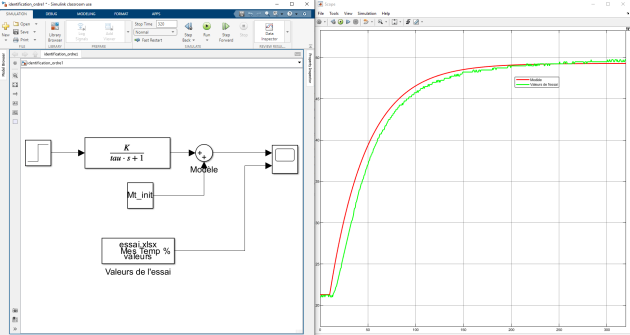
Q5. A l'aide de Matlab, réaliser un modèle d'ordre 1 avec la constante de temps trouvée précédemment, le gain identifié et comparer le modèle au relevé enregistré lors de l'expérimentation. Expliquer pourquoi ce modèle d’ordre 1 n’est pas suffisamment fidèle.
2.2.2. Modèle d’ordre 2 décomposable
Ce modèle correspond à une fonction de transfert de la forme : \(G_v(p)=\dfrac{\Delta M_T(p)}{\Delta S_r(p)}=\dfrac{G_{v0}}{(1+\tau_1 \, p)\,(1+\tau_2 \, p)}\).
Identification et comparaison
Q6. Déterminer par la méthode de Strejc-Broïda les valeurs des constantes de temps \(\tau_1\) et \(\tau_2\). Puis, à l'aide de Matlab, réaliser un modèle d'ordre 2 avec les constantes de temps trouvées, le gain identifié et comparer le modèle au relevé enregistré lors de l'expérimentation. Au besoin, affiner les valeurs des constantes de temps par la méthode des moindres carrés. Pour cela on pourra utiliser les outils proposés par le logiciel ‘Excel’ en exploitant le fichier de point enregistré sous le format *.txt.
Rappel :
Vous pouvez utiliser le fichier suivant comme lors du TD2.
Pensez à coller les valeurs de l'essai dans les deux premières colonnes (« t absolu » qui va de 0 à 320 s normalement et « MT relevée »).
Remplacer les lettres a, b, c et d par des valeurs judicieuses qui correspondent à votre essai.