Accélération, Vitesse, Déplacement
Un mouvement de translation (par exemple) s'effectue généralement en trois temps :
accélération
vitesse constante
décélération
Exemple : Trajet d'une nacelle transbordée (d'après sujet Métropole juin 2015)
Pour assurer le confort des usagers de la nacelle et minimiser le phénomène de ballant, le mouvement obéit à un profil de vitesse trapézoïdal :
accélération (constante)
déplacement à vitesse constante
décélération (constante)
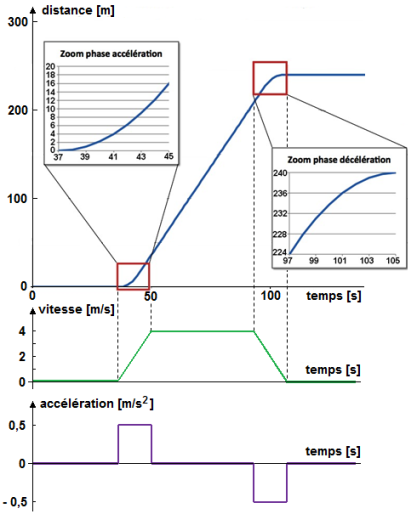
Les graphiques ci-dessous permettent d'observer que :
le déplacement se fait sans à-coup, il n'y a pas de brusque changement de pente s'agissant de la courbe distance = f(temps)
le déplacement à vitesse constante s'effectue à une vitesse \(v_{MAX}=4m \cdot s^{-1}\), ce qui correspond à 14,4km/h
la durée d'accélération (ou de décélération) est de 8s, pour une évolution de la vitesse (segment de droite) de 0 à 4m/s (ou de 4m/s à 0)
l'accélération \(acc\) est de ±0,5m/s2
Cette valeur est obtenue en faisant :
\(acc=\frac{v_{FINALE}-v_{INITIALE}}{t_{FINAL}-t_{INITIAL}}=\frac{4-0}{45-37}=0,5m\cdot s^{-2}\)
Remarque : Déplacement retour
Au retour, non représenté ci-dessus, la vitesse présenterait un profil similaire, avec toutefois des valeurs négatives, la vitesse est une grandeur algébrique.
Remarque : Vitesse moyenne
le déplacement proprement dit, hors phases de chargement/déchargement sur les quais, dure de t=37s à t=105s pour une distance totale parcourue de 240m, de quai à quai.
La vitesse moyenne du déplacement est donc :
\(v_{MOY}=\frac{d_{FINALE}-d_{INITIALE}}{t_{FINAL}-t_{INITIAL}}=\frac{240-0}{105-37}=3,53m\cdot s^{-1}\)
Cette vitesse moyenne est nécessairement inférieure à la vitesse \(v_{MAX}.\)