Vitesse du point
Vitesse du mouvement de translation
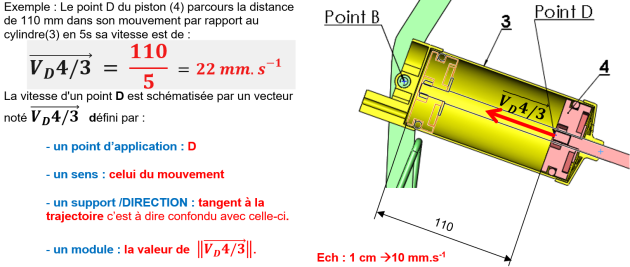
La vitesse moyenne du point D appartenant à un solide 4 par rapport au solide 3 est égale au rapport de la distance parcourue par le temps mis pour la parcourir. L'unité est m.s-1, cm.s-1, mm.s-1 ou km.h-1.
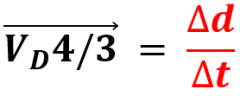
Vitesse instantanée (v)
Dans la formule précédente, plus Δt est petit, plus la vitesse moyenne se rapproche de la vitesse
instantanée. Celle-ci s'obtient par passage à la limite (Δt tendant vers 0, ou t1 tendant vers t0) et v est égale
à la dérivée de d par rapport au temps.
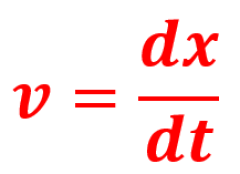
Vitesses angulaire du mouvement de rotation
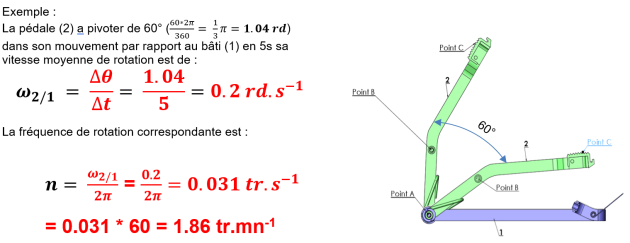
La vitesse angulaire moyenne (ω) du solide 2 par rapport au solide 1 est égale au
rapport de l'angle θ) parcouru par le temps (t) mis pour la parcourir. Les unités utilisées sont rd.s-1, rd.mn-1.
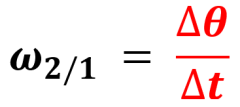
Fréquence de rotation (n)
Vitesse tangentielle
Elle correspond à la vitesse instantanée du point du solide en mouvement de rotation.
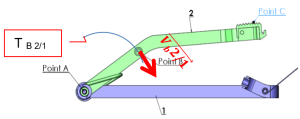
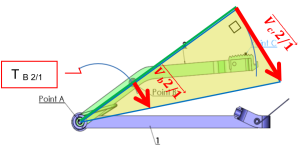
La vitesse du point B est schématisée par un vecteur noté (\overrightarrow {V_{B,2/1}}) ⃗ est défini par :
- un point d'application : B
- un sens : celui du mouvement
- un support : tangent à la trajectoire c'est à dire perpendiculaire au rayon AB .
- un module : la valeur de ‖\overrightarrow {V_{B,2/1}}‖ = (AB)*ω