Dilatation thermique
Les matériaux sont soumis à dilatation en raison de l'évolution de la température. Pour tous les matériaux isotropes la variation de longueur est donnée par la relation :
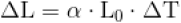
\(\Delta \mathrm{L}\) : allongement
\(\mathrm{L}_0\) : longueur initiale
\(\alpha\) : coefficient de dilatation, en \(K^{-1}.\)
\(\Delta \mathrm{T}\) : variation de température, en \(K\) ou en \(°C\) (inutile de convertir dans le cas d'une différence)
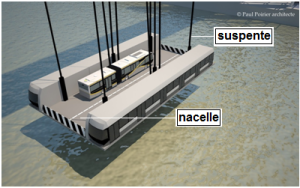
Exemple : Suspente de nacelle (d'après sujet Métropole juin 2015)
La nacelle d'un pont transbordeur est suspendue aux dessus des flots par dix câbles en acier appelés suspentes.
Les températures relevées pendant trente ans par la station météorologique voisine font état d'une température extrême :
minimale de -15.6°C (enregistrée lors d'un mois de février)
maximale de 40,3°C (enregistrée lors d'un mois de juillet)
Les suspentes ont une longueur initiale \(L_{0}=50m.\) Le coefficient de dilatation \(\alpha = 12 \, 10^{-6}K^{-1}.\)
La dilatation des suspentes est de :
\(\Delta L = \alpha \times L_{0} \times \Delta T = 12 \, 10^{-6} \times 50 \, 000 \times (40,3 - (-15.6)) = 33,5mm\)