Moment quadratique d'une poutre
Le moment quadratique (I) d'une poutre est exprimé en [mm4]. Il s'agit d'une grandeur qui caractérise la géométrie de la section droite de la poutre.
Ainsi, pour une poutre dont la section droite est rectangulaire, I varie selon que la poutre est sollicitée sur son plat ou sur son chant.
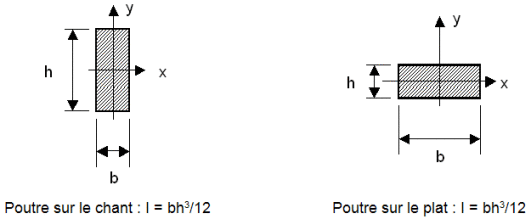
Remarque :
Si la relation reste la même, les valeurs numériques sont très différentes, le moment quadratique est beaucoup plus important dans le cas d'une poutre sollicitée sur son chant.
Exemple : Poutre en bois lamellé collé de section 150 mm x 800 mm.
Sur le plat, I ne vaut que 800 x 1503/12 = 225 000 000 mm4.
En revanche, quand cette poutre est sollicitée sur son chant, I = 150 x 8003/12 = 6 400 000 000 mm4, soit 640 000 cm4.
C'est évidemment cette seule valeur que l'on trouve dans les catalogues fournisseurs car cette poutre est faite pour être sollicitée dans ces conditions !
Fondamental :
Une poutre doit être positionnée sur le chant. La flèche \(f\) subie dépend en effet de :
\(L\) : portée de la poutre
\(E\) : module d'élasticité du matériau
\(I\) : moment quadratique de la section de la poutre
\(p\) : charge linéique
Si la relation diffère avec le cas de figure (poutre encastrée à une extrémité, en appui à l'autre par exemple) :
les termes E et I restent au dénominateur, il convient donc de les maximiser
le terme L reste au numérateur, il convient de le minimiser
Exemple : Poutre sur deux appuis soumise à une charge linéique uniforme
Pour une poutre sur deux appuis soumise à une charge linéique uniforme, la flèche \(f=\frac{5pL^{4}}{384EI}\)