Sollicitations - Contraintes - Déformations
Les sollicitations peuvent être simples ou composées (conjugaison de plusieurs sollicitations sur un même élément).
Exemple : Sollicitations simples
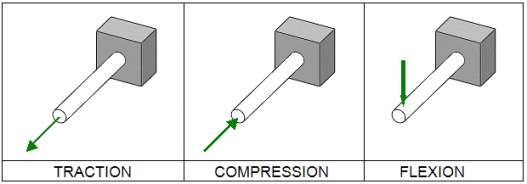
Sollicitations et Contraintes
Les sollicitations appliquées à un solide engendrent des contraintes dans le matériau. Une contrainte est homogène à une pression dans le matériau et s'exprime donc en N/m² ou en Pa (Pascal). Dans la pratique on utilise le MPa ou N/mm2.
Exemple : Contrainte - Solive en appui aux deux extrémités
Une solive en Épicéa de 22 x 8 cm est en appui aux deux extrémités sur deux poutres distantes de 4m. La charge linéique appliquée est de 800N/m.
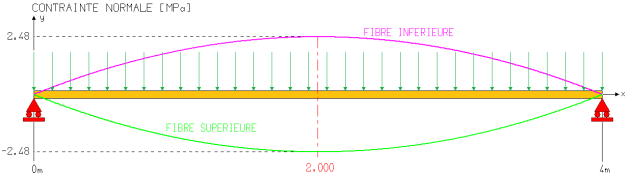
Une simulation a été effectuée grâce au logiciel RDM 6 LeMans (calcul des structures par la méthode des éléments finis) et a donné le résultat suivant (problème plan).
La contrainte est la plus forte en milieu de portée, soit en x = L/2 = 4m.
Les fibres de la solive ne se déforment pas de la même manière suivant y. Ainsi, si la fibre neutre a un allongement nul :
les fibres inférieures sont étirées, la contrainte est comptée positivement
les fibres supérieures sont comprimées, la contrainte est comptée négativement
La contrainte dans le matériau ne doit pas excéder la limite élastique.
Des logiciels de simulation peuvent donner une répartition volumique des contraintes grâce à un jeu de couleurs relié à une échelle de valeurs.
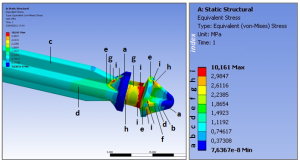
Exemple : Piston d'une pompe doseuse (d'après sujet Métropole juin 2014)
Une pompe doseuse est destinée à puiser dans un réservoir de l'engrais pour le mélanger à de l'eau dans un système d'irrigation autonome.
Le piston doseur est en polypropylène (PP) dont la limite élastique est de 22MPa. On peut vérifier que la contrainte maximum calculée est d'environ 10MPa, bien plus faible que la limite élastique du PP.
Sollicitation et Déformation
Un élément soumis à une sollicitation a tendance à se déformer.
Exemple : Déformation - Solive en appui aux deux extrémités
Une solive en Épicéa de 22 x 8 cm est en appui aux deux extrémités sur deux poutres distantes de 4m. La charge linéique appliquée est de 800N/m.
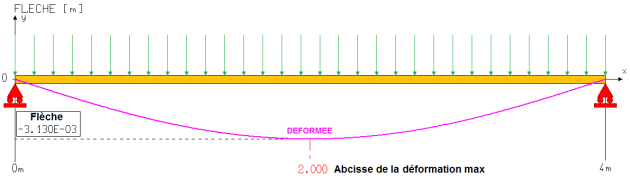
La même simulation que précédemment a donné le résultat suivant.
La déformée présente un maximum en x=2m, soit au milieu de la portée L. La flèche est de 3,1mm.
La solive est correctement dimensionnée car cette flèche reste inférieure à L/400.
Complément : ELS et ELU - Coefficient de Sécurité
Le dimensionnement d'une structure repose sur l'examen de deux situations :
ELS : État Limite de Service
ELU : État Limite Ultime
Par exemple, dans le cas d'un élément porteur horizontal (poutre) travaillant en flexion :
à l'ELS : on vérifie que la flèche reste inférieure à L/200, L/300, L/400,... (critères courants, il existe différents cas)
L : portée (distance entre appuis)
à l'ELU : on vérifie que la contrainte reste inférieure à la limite élastique avec un coefficient de sécurité \(CS = \frac {R_{e}}{\sigma}\)
\(R_{e}\) : limite élastique du matériau
\(\sigma\) : contrainte
CS doit être supérieur à 1.