Limite élastique et Module de Young
Lors d'un essai de traction, on fait subir à une éprouvette une contrainte (« sigma ») \(\sigma=\frac{F}{S_{0}}\)
où F est la force exercée (en newtons [N]) et S0 la section droite initiale. La contrainte s'exprime donc en N/mm².
Il s'ensuit un allongement de l'éprouvette (déformation).
Pour comparer les phénomènes et les matériaux, on s'intéresse plutôt à l'allongement relatif qui est sans unité.
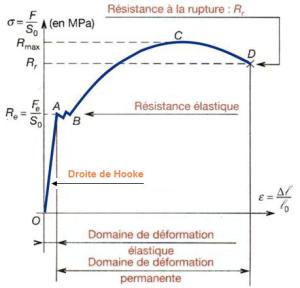
La courbe représentant la contrainte en fonction de l'allongement relatif a généralement l'allure suivante.
Le début de la courbe, connue sous le nom de loi de Hooke, traduit le comportement élastique du matériau : si on supprime l'effort de traction, le matériau retrouve ses dimensions initiales. Il y a, dans cette zone, proportionnalité entre la contrainte exercée et l'allongement relatif, le coefficient de proportionnalité (E) étant appelé module d'élasticité ou module de Young.
\(\sigma = E \times \epsilon\)
Le module d'élasticité s'exprime en N/mm² équivalent au MPa.
Au delà de cette limite élastique, on rentre dans le domaine plastique, qui va jusqu'à la rupture en passant par différents stades.
Exemple : Acier S235
Limite élastique : Re = 235 MPa (ou 235 N/mm²)
Module de Young : E = 210 000 MPa, soit 210 GPa
Fondamental : MPa - N/mm²
MPa : Abréviation de MégaPascal (unité)
En RDM (Résistance Des Matériaux), le module de Young (ou module d'élasticité) est exprimé en méga-Pascal [MPa].
Un Pascal est défini comme une force de 1 Newton exercée sur une surface de 1m². Par conséquent :
1MPa = 1N/mm²
Cela conduit à exprimer les dimensions en mm, les sections en mm2, les moments quadratiques en mm4.