Trajectoire
Définition : Trajectoire
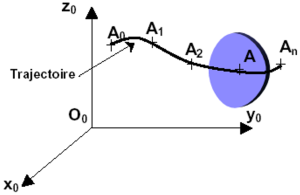
Soit A un point du solide (S) : lors du mouvement de (S), il occupe un ensemble de positions successives dans le repère de référence \(\mathfrak{R}_{0}\) au cours du temps. Cet ensemble de positions est la trajectoire du point A dans le mouvement de (S) par rapport à \(\mathfrak{R}_{0}\).
On la désigne : \(T_{A(S/R_0)}\) ou \(T_{A \in S/R_0}\).
La trajectoire est la « trace » laissée par le point au cours du temps.
Cela peut-être :
un arc de cercle d'axe (un point + un vecteur), de centre (un point) et de rayon (un segment) ;
un segment de droite porté par la droite (un point + un vecteur) ;
un point ;
une courbe quelconque.
Définition : Rotation d'axe fixe - Liaison pivot
Les trajectoires de points fixes dans un solide en mouvement de rotation autour d'un axe fixe (liaison pivot) sont des arcs de cercle de même axe.
Définition : Translation rectiligne - Liaison glissière
Les trajectoires de points fixes dans un solide en mouvement de translation à trajectoire rectiligne (liaison glissière) sont des segments de droite.
Définition : Translation circulaire
Les trajectoires de points fixes dans un solide en mouvement de translation à trajectoire circulaire sont des arcs de cercle de même rayon.
Trajectoire d'un point géométrique de contact – Notion de points coïncidents
Les positions successives A0, A1, A2, ... , An du point A dans \(\mathfrak{R}_{0}\) sont appelés points coïncidents de A aux instants t0, t1, t2, ... , tn.
Définir la trajectoire c'est définir l‘ensemble des points coïncidents.
En un point géométrique de contact P entre deux solides 1 et 2, on distingue 3 points coïncidents à un instant t :
P∈1 ⟸ point fixe dans 1
P∈2 ⟸ point fixe dans 2
P∉1 et P∉1 ⟸ point géométrique de contact
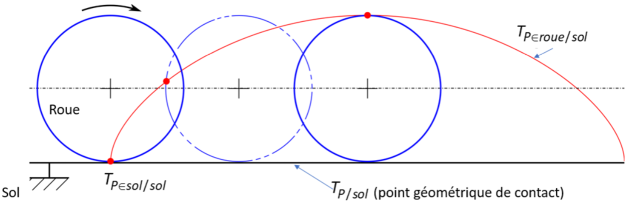
Au point de contact P entre la roue et le sol, on distingue :
P∈sol : c'est le gravillon fixe du bitume, sa trajectoire par rapport au sol est un point (lui-même) ;
P∈roue : c'est la valve de la roue (par exemple), sa trajectoire par rapport au sol est une cycloïde ;
P : point géométrique de contact, sa trajectoire appartient au sol (elle représente les positions successives prises par le point géométrique de contact entre la roue et le sol).
Pour déterminer la trajectoire d'un point géométrique de contact dans un repère, il sera nécessaire de déterminer l'expression de son vecteur position dans ce repère.
Exemple : Bicyclette
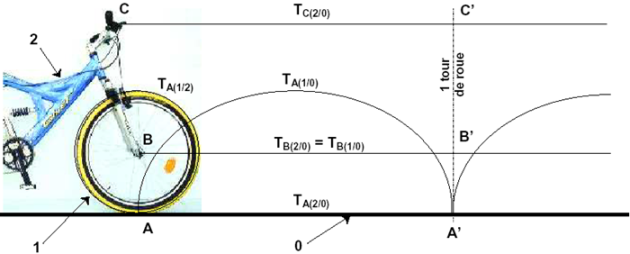
Soit A le point de contact entre la roue 1 et le sol 0.
Soit B le centre de l'articulation entre la roue 1 et le cadre 2.
Soit C un point appartenant au cadre 2.
On peut noter la nature des trajectoires suivantes :
\(T_{C \in 2/0}\). : droite horizontale (rectiligne horizontale)
\(T_{B \in 1/2}\) : point coïncident (fixe)
\(T_{B \in 1/0}\) : droite horizontale
\(T_{B \in 2/0}\) : droite horizontale
\(T_{A \in 2/0}\) : droite horizontale
\(T_{A \in 1/2}\) : cercle de centre B et de rayon BA
\(T_{A \in 1/0}\) : cycloïde