Loi de commande en position
Particularité des bases dans un mouvement de translation
Dans le cas d'un mouvement de translation entre deux solides 1 et 2, les bases sont identiques : \((\vec{x_1},\vec{y_1},\vec{z_1})=(\vec{x_2},\vec{y_2},\vec{z_2})\) ou B1=B2, mais \(\mathfrak{R}_{1} \neq \mathfrak{R}_{2}\).
Paramètre de mouvement d'une liaison glissière
Une liaison glissière de direction \(\vec{x_1}\) entre deux solides 1 et 2, est paramétrée par la longueur \(\lambda (t)\) tel que \(\overrightarrow{0_{\in1}M_{\in2}}=\lambda (t) \vec{x_1}\).
Dans l'exemple ci-contre, le mouvement de translation à trajectoire rectiligne de la cabine 2 par rapport à la station 1 est de direction \(\vec{x_1}=\vec{x_2}\).
Paramètre de mouvement d'une liaison pivot
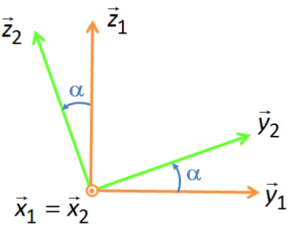
Une liaison pivot d'axe \((A,\vec{x})\) entre deux solides 1 et 2, est paramétrée par un angle \(\alpha(t)\) en radian tel que : \(\alpha(t)=(\vec{y_1},\vec{y_2})=(\vec{z_1},\vec{z_2})\).
Cet angle oriente à chaque instant, la base \(B_2=(\vec{x_2},\vec{y_2},\vec{z_2})\) par rapport à la base \(B_1=(\vec{x_1},\vec{y_1},\vec{z_1})\).
Il est représenté par une figure de changement de base.
Paramètre caractéristique
Contrairement aux paramètres de mouvement qui sont variables, les paramètres caractéristiques sont les paramètres constants qui influent sur le mouvement.
Ce sont en général des paramètres géométriques (longueurs de solides, entraxes...).
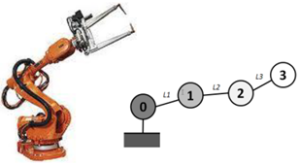
Commande des mécanismes en chaîne ouverte
Les paramètres de mouvement sont tous indépendants.
Chaque liaison est « motrice » et est commandée par sa propre chaîne d'énergie-puissance (actionneur, ...).
Dans l'exemple ci-contre, il existe 3 liaisons « motrices », et donc 3 chaînes d'énergie-puissance (3 actionneurs...).
Commande des mécanismes en chaîne fermée
Les paramètres de mouvement sont tous dépendants.
Ainsi, une seule liaison est alors « motrice ». Une seule chaîne d'énergie-puissance existe (actionneur, ...).
Dans l'exemple ci-contre, il existe 1 liaison « motrice », et donc 1 chaîne d'énergie-puissance (1 actionneur...).
Vecteur position d'un point M fixe dans un solide S par rapport à un solide de référence 0
Un vecteur position d'un point M fixe dans un solide S, dans son mouvement par rapport à un solide de référence 0, est un vecteur \(\overrightarrow{Q_{\in0}M_{\in S}}\) avec Q_(∈0) un point fixe dans le repère associé au solide de référence 0, en général l'origine.
Exemple : robot industriel
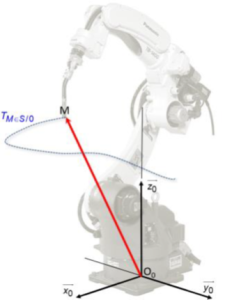
Dans le repère \(\mathfrak{R}_{0}(O_0,\vec{x_0},\vec{y_0},\vec{z_0})\) associé au solide de référence, à la date t :
un vecteur position de M est \(\overrightarrow{O_{\in0}M_{\in S}}(t)\)
Lorsqu'il n'y pas d'ambiguïté sur le fait qu'un point est fixe dans un solide (centre de gravité d'un solide, origine d'un repère associé à un solide, centre d'une liaison...), il n'est pas utile de le préciser dans la notation. Dans notre exemple : \(\overrightarrow{O_{\in0}M_{\in S}}(t)=\overrightarrow{O_{\in0}M}(t)\)
Pour alléger les notations, il est fréquent de ne pas écrire la variable t.
La courbe ainsi définie par ce vecteur position correspond à la trajectoire \(T_{M \in S/R_0}\).
