Séquence 6

Une force distante d'un axe, crée un moment autour de cet axe. La force \(\overrightarrow {F1_{utilisateur \rightarrow poignee}} \)tend à faire tourner la poignée autour de l'axe (A, \({\vec{z}}\)) mais pas \(\overrightarrow {F2_{utilisateur \rightarrow poignee}} \).

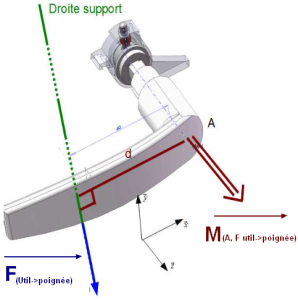
Un moment sera représenté par un vecteur suivant les règles suivantes :

• double trait appliqué au point A,

• de direction perpendiculaire au plan formé par le point A et la force \({\vec{F}}\) (axe autour duquel aurait tendance à s'effectuer la rotation)

• de sens positif si la force F fait tourner le point A dans le sens trigonométrique (de x->y, ou de y->z, ou de z->x) et négatif dans le cas contraire

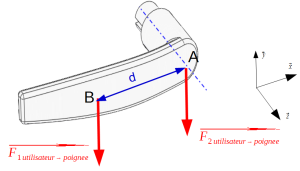
• de norme : M_{(A,Futil->poignée)} = d x F avec d = distance de A à la force F, mesurée perpendiculairement de A à F, encore appelée bras de levier

Notation : \(\overrightarrow {M_{(A,util \rightarrow poignee)}} \left( \begin{array}{c}0 \\0 \\ + d F\\\end{array} \right) \)ou \(\overrightarrow {M_{(A,util \rightarrow poignee)}} =0\vec{x} +0\vec{y} + d F\vec{z}\)