5. Lien entre actions mécaniques et mouvements
Présentation du système
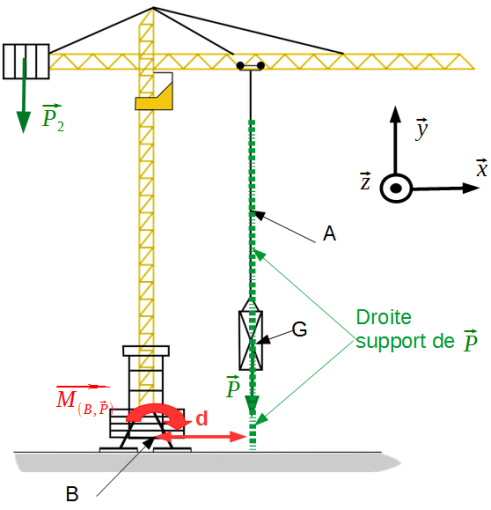
La figure ci-dessous représente une charge soutenue par une grue.
La terre exerce une action mécanique sur la charge modélisable par une force au point G : le poids \(\vec P\).
On obtient la modélisation suivante :
\(\mathcal{T} _{terre \rightarrow charge} = \begin{array} {c}\\ \\\\\end{array} _G {\left\{ \begin{array} {cc}\overrightarrow {P_{ charge}}=0 \vec x-P \vec y + 0 \vec z\\\overrightarrow {M_{(G,terre \rightarrow charge)}}= 0 \vec x+0\vec y +0 \vec z\\\end{array} \right\} }\)
Remarque : Lien entre résultante et mouvement de translation
Le point A est situé sur la droite support de \(\vec P\) donc \(\overrightarrow {M_{(A,\vec P)}}= \vec0\).
La modélisation devient :
\(\mathcal{T} _{terre \rightarrow charge} = \begin{array} {c}\\ \\\\\end{array} _A {\left\{ \begin{array} {cc}\overrightarrow {P_{ charge}}=0 \vec x-P \vec y + 0 \vec z\\\overrightarrow {M_{(A,terre \rightarrow charge)}}= 0 \vec x+0\vec y +0 \vec z\\\end{array} \right\} }\)
Dans la réalité, la charge tend à provoquer un mouvement de translation sur\( \vec y\) du câble.
On constate qu'une force ou résultante tend à créer ou empêcher un mouvement de translation.
Remarque : Lien entre moment et mouvement de rotation
Le point B n'est pas situé sur la droite support de \(\vec P\) mais à une distance d. Donc \(\overrightarrow {M_{(B,\vec P)}}= -d.P \vec z\).
La modélisation devient :
\(\mathcal{T} _{terre \rightarrow charge} = \begin{array} {c}\\ \\\\\end{array} _B {\left\{ \begin{array} {cc}\overrightarrow {P_{ charge}}=0 \vec x-P \vec y + 0 \vec z\\\overrightarrow {M_{(B,terre \rightarrow charge)}}= 0 \vec x+0\vec y -d.P \vec z\\\end{array} \right\} }\)
Dans la réalité, la charge tend à provoquer un mouvement de rotation autour de l'axe \((B,\vec z)\) de la grue.
On constate qu'un moment tend à créer ou empêcher un mouvement de rotation.