Génération de valeurs aléatoires suivant une loi
La génération de valeurs aléatoires suivant une loi de probabilité donnée fait appel à l’expression des fonctions réciproques des fonctions de répartition des lois de probabilité considérées.
Cas d’une loi uniforme ou rectangulaire
La fonction réciproque de la fonction de répartition associée à une loi uniforme s’écrit :
\(x=a \times \Biggl[ 2F(x)-1 \Biggr]\) avec \(0 \leq F(x) \leq 1\)
Soit pour générer les éléments d’une suite respectant une loi uniforme :
\(x_n=a \times [ 2\, u_n-1 ]\, + \, b\)
Dans cette dernière relation, l’erreur maximale tolérée (EMT) est notée a et b représente le centre de l’intervalle de définition de la loi.
Cas d’une loi triangulaire isocèle
La fonction réciproque de la fonction de répartition associée à une loi triangulaire isocèle s’écrit :
\(\begin{cases} x=a\Bigl[ \, \sqrt[]{2\, F_G(x)}-1 \Bigr] \quad \text{avec} \quad 0,0 \leq F_G(x)\leq0,5 \\ x=a\Bigl[ \,1-\, \sqrt[]{2\,(1- F_D(x))} \Bigr] \quad \text{avec} \quad 0,5 \leq F_D(x)\leq1 \end{cases}\)
Soit pour générer les éléments d’une suite respectant une loi triangulaire isocèle :
\(\begin{cases} x_n=a\biggl[ \, \sqrt[]{2\, u_n}-1 \biggr]+b \quad \text{avec} \quad 0,0\leq u_n \leq0,5 \\ x=a\biggl[ \,1-\, \sqrt[]{2\,(1- u_n)} \biggr]+b \quad \text{avec} \quad 0,5\leq u_n\leq1 \end{cases}\)
Dans cette dernière relation, l’erreur maximale tolérée (EMT) est notée a et b représente le centre de l’intervalle de définition de la loi.
Cas d’une loi dérivée d’arc-sinus
La fonction réciproque de la fonction de répartition associée à une loi triangulaire isocèle s’écrit :
\(x=-a \times cos[\pi \, F(x)] \quad \text{avec} \quad 0 \leq F(x)\leq 1\)
Soit pour générer les éléments d’une suite respectant une loi triangulaire isocèle :
\(x_n=-a \times \cos ( \pi \, u_n)\, + \, b\)
Dans cette dernière relation, l’erreur maximale tolérée (EMT) est notée a et b représente le centre de l’intervalle de définition de la loi.
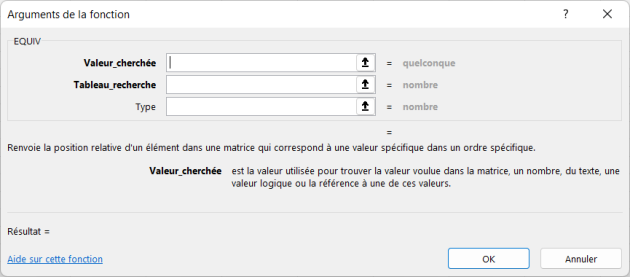
Utilisation de la fonction =EQUIV() et de la fonction =CHOISIR()
La fonction =EQUIV() permet d’associer un nombre entier naturel au type de loi choisi à partir de la validation de données. Dans la recherche d’une chaîne de caractères (texte), il convient d’imposer la stricte correspondance entre la valeur recherchée et les valeurs présentes dans le tableau de recherche. Il convient d’associer dans ce cas la valeur zéro dans l’argument « Type » de la fonction.
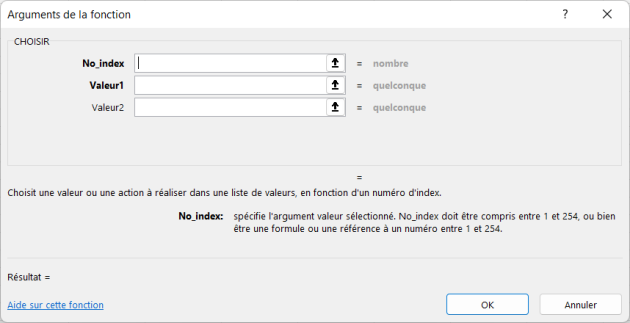
La fonction =CHOISIR() évite une importante imbrication de fonctions conditionnelles dans le cadre de ce projet ; le numéro d’index correspond au résultat renvoyé par la fonction =EQUIV().
Les différentes « valeurs » à renvoyer comme résultat correspondent aux équations des fonctions réciproques des fonctions de répartition présentées précédemment.