Régulation de TEMPERATURE - SYSTEME « Habilis »

On considère le processus seul (résistances de chauffage du malaxeur) dont :

▪ L’entrée de commande notée \(u(t)\) est une information analogique relative à la sortie du correcteur PID ;

▪ La sortie notée \(\theta(t)\) est la température mesurée par la sonde ;

▪ La température ambiante notée \(\theta_{amb}(t)\) est une entrée de perturbation.

Q1. Représenter un schéma bloc de ce processus seul qui fasse apparaître \(u(t)\), \(\theta(t)\) et \(\theta_{ambt}(t)\).

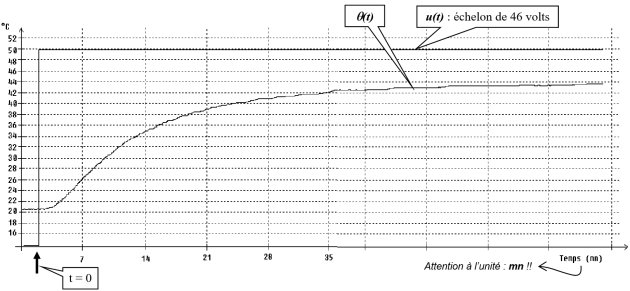
On a relevé l’évolution de la température \(\theta(t)\) suite à un échelon de tension \(u(t)\) égal à 20% de Umax= 230 V :

Compte tenu de cette évolution, on peut modéliser le processus par la fonction de transfert suivante (1° ordre avec retard) :

\(H(p)=\dfrac{\theta(t)-\theta_{amb}}{u(t)}=\dfrac{G_S.e^{-Tp}}{1+\tau p}\)

Q2. Appliquer la méthode de Broïda afin de déterminer les valeurs numériques des coefficients \(G_S\), \(T\) et \(\tau\) qui apparaissent dans cette modélisation (attention : \(T\) et \(\tau\) devront être exprimés en secondes !)